We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In [3] we initiated our study of the automorphism groups of a certain class of near-rings. Specifically, let P be any complex polynomial and let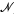 
P denote the near-ring of all continuous selfmaps of the complex plane where addition of functions is pointwise and the product fg of two functions f and g in 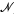P is defined by fg=f∘P∘g. The near-ring 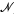P is referred to as a laminated near-ring with laminating element P. In [3], we characterised those polynomials P(z)=anzn + an−1zn−1 +…+a0 for which Aut 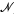P is a finite group. We are able to show that Aut 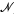P is finite if and only if Deg P≧3 and ai ≠ 0 for some i ≠ 0, n. In addition, we were able to completely determine those infinite groups which occur as automorphism groups of the near-rings 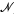P. There are exactly three of them. One is GL(2) the full linear group of all real 2×2 nonsingular matrices and the other two are subgroups of GL(2). In this paper, we begin our study of the finite automorphism groups of the near-rings 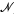P. We get a result which, in contrast to the situation for the infinite automorphism groups, shows that infinitely many finite groups occur as automorphism groups of the near-rings under consideration. In addition to this and other results, we completely determine Aut 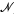P when the coefficients of P are real and Deg P = 3 or 4.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.
Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.
To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.
