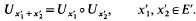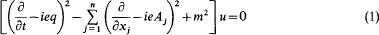Research Article
Angular momentum, convex Polyhedra and Algebraic Geometry
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 121-133
-
- Article
-
- You have access
- Export citation
The mean value theorem and analytic functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 289-295
-
- Article
-
- You have access
- Export citation
Functorial radicals and non-abelian torsion, II
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
Finite automorphism groups of laminated near-rings
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 297-306
-
- Article
-
- You have access
- Export citation
The first hundred years (1883–1983)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 135-150
-
- Article
-
- You have access
- Export citation
The partially ordered family of all ℛ-classes of S(x)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 7-13
-
- Article
-
- You have access
- Export citation
Cauchy problems for second order hyperbolic differential equations with constant coefficients
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 307-311
-
- Article
-
- You have access
- Export citation
The syntactic near-ring of a linear sequential machine
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 15-24
-
- Article
-
- You have access
- Export citation
Epis are onto for finite regular semigroups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 151-162
-
- Article
-
- You have access
- Export citation
An algebraic filtration of H*(MO;ℤ2)
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 313-317
-
- Article
-
- You have access
- Export citation
On quasinormal subgroups of certain finitely generated groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 25-28
-
- Article
-
- You have access
- Export citation
Semi-embeddings of Banach spaces which are hereditarily c0
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 163-167
-
- Article
-
- You have access
- Export citation
A note an homeomorphic measures on topological groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 169-171
-
- Article
-
- You have access
- Export citation
Some bifurcation problems in cholesteric liquid crystal theory
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 319-332
-
- Article
-
- You have access
- Export citation
Isomorphisms between spaces of vector-valued continuous functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 29-48
-
- Article
-
- You have access
- Export citation
A singular perturbation problem for the Lavrent'ev-Bitsadze equation*
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 49-66
-
- Article
-
- You have access
- Export citation
Free resolutions for certain classes of groups
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 173-179
-
- Article
-
- You have access
- Export citation
A stochastic proof of an extension of a theorem of Rado
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 333-336
-
- Article
-
- You have access
- Export citation
Unitary representations corresponding to measures with bounded support in infinite dimensions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 67-72
-
- Article
-
- You have access
- Export citation
Eigenvalues of the Klein-Gordon equation
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 181-190
-
- Article
-
- You have access
- Export citation



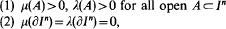
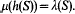
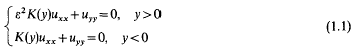
 of φ at
of φ at