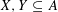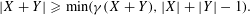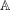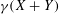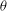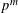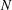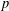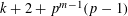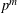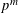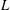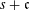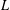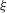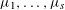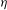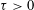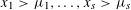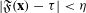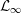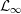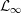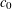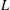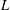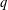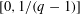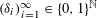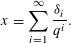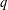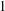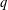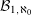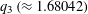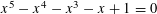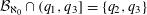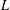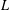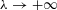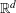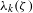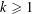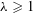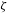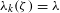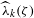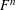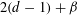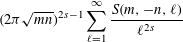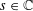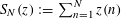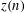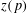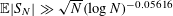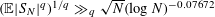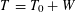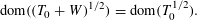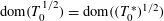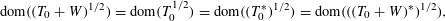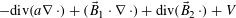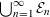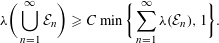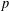Research Article
CAUCHY–DAVENPORT TYPE THEOREMS FOR SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2015, pp. 1-12
-
- Article
- Export citation
A GENERALIZATION OF THE DISCRETE VERSION OF MINKOWSKI’S FUNDAMENTAL THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 29 February 2016, pp. 637-652
-
- Article
- Export citation
ON THE THETA OPERATOR FOR MODULAR FORMS MODULO PRIME POWERS
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 321-336
-
- Article
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
-
- Article
- Export citation
INTERMEDIATE SUMS ON POLYHEDRA II: BIDEGREE AND POISSON FORMULA
- Part of:
-
- Published online by Cambridge University Press:
- 29 February 2016, pp. 653-684
-
- Article
- Export citation
WARING’S PROBLEM WITH SHIFTS
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2015, pp. 13-46
-
- Article
- Export citation
ON SUMS OF FOUR SQUARES OF PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 348-361
-
- Article
- Export citation
ON THE STRUCTURE OF SEPARABLE
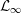 ${\mathcal{L}}_{\infty }$-SPACES
${\mathcal{L}}_{\infty }$-SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2016, pp. 685-700
-
- Article
- Export citation
SPECIAL VALUES OF SHIFTED CONVOLUTION DIRICHLET SERIES
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2015, pp. 47-66
-
- Article
- Export citation
ON SMALL BASES FOR WHICH 1 HAS COUNTABLY MANY EXPANSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 362-377
-
- Article
- Export citation
THE DISTRIBUTION OF 2-SELMER RANKS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH PARTIAL TWO-TORSION
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2015, pp. 67-78
-
- Article
- Export citation
SPECTRAL THEORETIC CHARACTERIZATION OF THE MASSLESS DIRAC ACTION
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 701-718
-
- Article
-
- You have access
- Open access
- Export citation
DECOMPOSITION OF BALLS IN
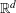 $\mathbb{R}^{d}$
$\mathbb{R}^{d}$
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 378-405
-
- Article
- Export citation
SOME SHARP BILINEAR SPACE–TIME ESTIMATES FOR THE WAVE EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2016, pp. 719-737
-
- Article
- Export citation
ON THE SPECTRUM OF DIOPHANTINE APPROXIMATION CONSTANTS
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2015, pp. 79-100
-
- Article
- Export citation
UNIONS OF LINES IN
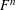 $F^{n}$
$F^{n}$
- Part of:
-
- Published online by Cambridge University Press:
- 11 April 2016, pp. 738-752
-
- Article
- Export citation
OPPOSITE-SIGN KLOOSTERMAN SUM ZETA FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 406-429
-
- Article
- Export citation
HELSON’S PROBLEM FOR SUMS OF A RANDOM MULTIPLICATIVE FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 21 October 2015, pp. 101-110
-
- Article
- Export citation
ON STABILITY OF SQUARE ROOT DOMAINS FOR NON-SELF-ADJOINT OPERATORS UNDER ADDITIVE PERTURBATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2015, pp. 111-182
-
- Article
- Export citation
THE DUFFIN–SCHAEFFER-TYPE CONJECTURES IN VARIOUS LOCAL FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2016, pp. 753-800
-
- Article
- Export citation