Article contents
SPECIAL VALUES OF SHIFTED CONVOLUTION DIRICHLET SERIES
Published online by Cambridge University Press: 16 June 2015
Abstract
In a recent important paper, Hoffstein and Hulse [Multiple Dirichlet series and shifted convolutions, arXiv:1110.4868v2] generalized the notion of Rankin–Selberg convolution 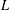 $L$-functions by defining shifted convolution
$L$-functions by defining shifted convolution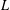 $L$-functions. We investigate symmetrized versions of their functions, and we prove that the generating functions of certain special values are linear combinations of weakly holomorphic quasimodular forms and “mixed mock modular” forms.
$L$-functions. We investigate symmetrized versions of their functions, and we prove that the generating functions of certain special values are linear combinations of weakly holomorphic quasimodular forms and “mixed mock modular” forms.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2015
References
- 4
- Cited by




