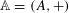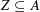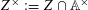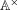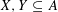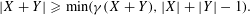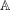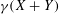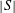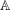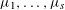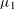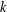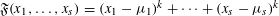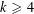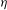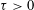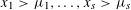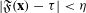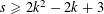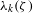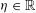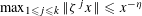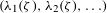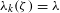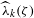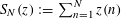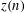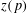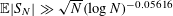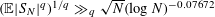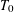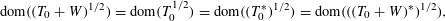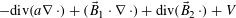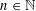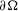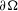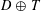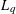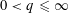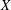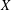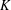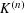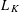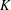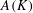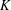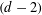For Jeff Hoffstein on his 61st birthday
Research Article
CAUCHY–DAVENPORT TYPE THEOREMS FOR SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2015, pp. 1-12
-
- Article
- Export citation
WARING’S PROBLEM WITH SHIFTS
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2015, pp. 13-46
-
- Article
- Export citation
SPECIAL VALUES OF SHIFTED CONVOLUTION DIRICHLET SERIES
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2015, pp. 47-66
-
- Article
- Export citation
THE DISTRIBUTION OF 2-SELMER RANKS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH PARTIAL TWO-TORSION
- Part of:
-
- Published online by Cambridge University Press:
- 04 May 2015, pp. 67-78
-
- Article
- Export citation
ON THE SPECTRUM OF DIOPHANTINE APPROXIMATION CONSTANTS
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2015, pp. 79-100
-
- Article
- Export citation
HELSON’S PROBLEM FOR SUMS OF A RANDOM MULTIPLICATIVE FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 21 October 2015, pp. 101-110
-
- Article
- Export citation
ON STABILITY OF SQUARE ROOT DOMAINS FOR NON-SELF-ADJOINT OPERATORS UNDER ADDITIVE PERTURBATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2015, pp. 111-182
-
- Article
- Export citation
DYADIC SHIFT RANDOMIZATION IN CLASSICAL DISCREPANCY THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2015, pp. 183-209
-
- Article
- Export citation
ISOSPECTRALITY FOR GRAPH LAPLACIANS UNDER THE CHANGE OF COUPLING AT GRAPH VERTICES: NECESSARY AND SUFFICIENT CONDITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2015, pp. 210-242
-
- Article
- Export citation
LEVEL SETS OF THE RESOLVENT NORM OF A LINEAR OPERATOR REVISITED
- Part of:
-
- Published online by Cambridge University Press:
- 26 June 2015, pp. 243-265
-
- Article
- Export citation
CONCAVITY PROPERTIES OF EXTENSIONS OF THE PARALLEL VOLUME
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2015, pp. 266-282
-
- Article
- Export citation
THE VOLUME OF RANDOM POLYTOPES CIRCUMSCRIBED AROUND A CONVEX BODY
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2015, pp. 283-306
-
- Article
- Export citation
A SIMPLICIAL POLYTOPE THAT MAXIMIZES THE ISOTROPIC CONSTANT MUST BE A SIMPLEX
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2015, pp. 307-320
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 62 Issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 December 2015, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
MTK volume 62 Issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 December 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation