Article contents
THE DISTRIBUTION OF 2-SELMER RANKS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH PARTIAL TWO-TORSION
Published online by Cambridge University Press: 04 May 2015
Abstract
This paper presents a new result concerning the distribution of 2-Selmer ranks in the quadratic twist family of an elliptic curve over an arbitrary number field 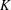 $K$ with a single point of order two that does not have a cyclic 4-isogeny defined over its two-division field. We prove that at least half of all the quadratic twists of such an elliptic curve have arbitrarily large 2-Selmer rank, showing that the distribution of 2-Selmer ranks in the quadratic twist family of such an elliptic curve differs from the distribution of 2-Selmer ranks in the quadratic twist family of an elliptic curve having either no rational two-torsion or full rational two-torsion.
$K$ with a single point of order two that does not have a cyclic 4-isogeny defined over its two-division field. We prove that at least half of all the quadratic twists of such an elliptic curve have arbitrarily large 2-Selmer rank, showing that the distribution of 2-Selmer ranks in the quadratic twist family of such an elliptic curve differs from the distribution of 2-Selmer ranks in the quadratic twist family of an elliptic curve having either no rational two-torsion or full rational two-torsion.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2015
References
- 5
- Cited by


