Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 355
The maximum numbers of faces of a convex polytope
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 179-184
-
- Article
-
- You have access
- Export citation
- Cited by 306
Rational approximations to algebraic numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-20
-
- Article
-
- You have access
- Export citation
- Cited by 258
On irregularities of distribution
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-79
-
- Article
- Export citation
- Cited by 221
On the flow near the trailing edge of a flat plate II
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-121
-
- Article
- Export citation
- Cited by 209
A Slow motion of viscous liquid caused by a slowly moving solid sphere
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-74
-
- Article
-
- You have access
- Export citation
- Cited by 187
The large sieve
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-134
-
- Article
- Export citation
- Cited by 184
The realization of distances within sets in Euclidean space
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-24
-
- Article
- Export citation
- Cited by 160
A slow motion of viscous liquid caused by the rotation of a solid sphere
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 13-24
-
- Article
- Export citation
- Cited by 155
On the large sieve
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-225
-
- Article
- Export citation
- Cited by 147
On the slow motion generated in a viscous fluid by the approach of a sphere to a plane wall or stationary sphere
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 37-49
-
- Article
- Export citation
- Cited by 147
Generation of acoustic pulses by baffled plane pistons
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 209-224
-
- Article
- Export citation
- Cited by 144
Linear forms in the logarithms of algebraic numbers
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 204-216
-
- Article
- Export citation
- Cited by 143
Shapes of worn stones
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-11
-
- Article
- Export citation
- Cited by 141
Approximate subdifferentials and applications 3: the metric theory
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-38
-
- Article
- Export citation
- Cited by 130
On the Hankel determinants of univalent functions
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 108-112
-
- Article
- Export citation
- Cited by 117
On the units of algebraic number fields
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 121-124
-
- Article
- Export citation
- Cited by 114
Asymptotic expansions and inequalities for hypergeometric function
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 278-301
-
- Article
- Export citation
- Cited by 113
Oscillating viscous flows
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 161-175
-
- Article
- Export citation
- Cited by 111
The distribution of quadratic residues and non-residues
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 106-112
-
- Article
- Export citation
- Cited by 105
On the Interaction between two identical neutral dipole systems, One in an excited state and the other in the ground state
-
- Published online by Cambridge University Press:
- 26 February 2010, pp. 91-94
-
- Article
- Export citation

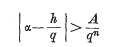



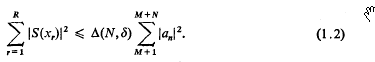
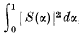 where
where 
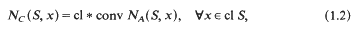
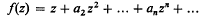
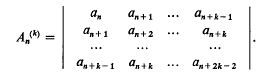
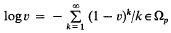
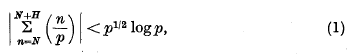
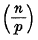 being Legendre's symbol of quadratic character.
being Legendre's symbol of quadratic character.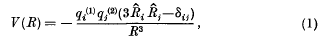
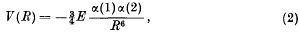
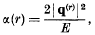
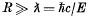 was given by Casimir and Polder as
was given by Casimir and Polder as