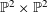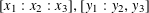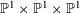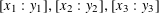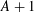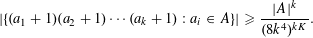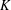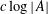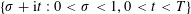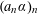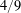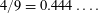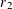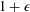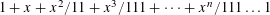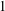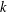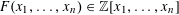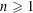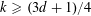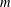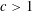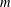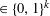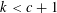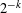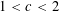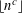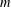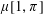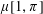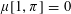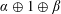Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
THE POWER-SAVING MANIN–PEYRE CONJECTURE FOR A SENARY CUBIC
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2019, pp. 789-830
-
- Article
- Export citation
ON ITERATED PRODUCT SETS WITH SHIFTS
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 831-850
-
- Article
- Export citation
ON SIMPLE ZEROS OF THE DEDEKIND ZETA-FUNCTION OF A QUADRATIC NUMBER FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2019, pp. 851-861
-
- Article
- Export citation
A CONVERSE THEOREM WITHOUT ROOT NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 862-873
-
- Article
- Export citation
ON THE INTEGRAL FORMULAS OF CROFTON AND HURWITZ RELATIVE TO THE VISUAL ANGLE OF A CONVEX SET
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2019, pp. 874-896
-
- Article
- Export citation
A CERTAIN DIRICHLET SERIES OF RANKIN–SELBERG TYPE ASSOCIATED WITH THE IKEDA LIFT OF HALF-INTEGRAL WEIGHT
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2019, pp. 897-928
-
- Article
- Export citation
THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 23 July 2019, pp. 929-949
-
- Article
- Export citation
AN EXPLICIT TWO-SOURCE EXTRACTOR WITH MIN-ENTROPY RATE NEAR
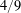 $4/9$
$4/9$
- Part of:
-
- Published online by Cambridge University Press:
- 24 July 2019, pp. 950-957
-
- Article
- Export citation
FLAG AREA MEASURES
- Part of:
-
- Published online by Cambridge University Press:
- 23 July 2019, pp. 958-989
-
- Article
- Export citation
THE MAXIMAL ORDER OF ITERATED MULTIPLICATIVE FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 30 July 2019, pp. 990-1009
-
- Article
- Export citation
FINITE FLAT SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1010-1017
-
- Article
- Export citation
INTERVALS BETWEEN CONSECUTIVE NUMBERS WHICH ARE SUMS OF TWO SQUARES
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1018-1032
-
- Article
- Export citation
A CLASS OF IRREDUCIBLE POLYNOMIALS ASSOCIATED WITH PRIME DIVISORS OF VALUES OF CYCLOTOMIC POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1033-1037
-
- Article
- Export citation
DENSITY OF POWER-FREE VALUES OF POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1038-1050
-
- Article
- Export citation
RANDOMNESS AND NON-RANDOMNESS PROPERTIES OF PIATETSKI-SHAPIRO SEQUENCES MODULO
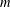 $m$
$m$
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1051-1073
-
- Article
- Export citation
ZEROS OF THE MÖBIUS FUNCTION OF PERMUTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1074-1092
-
- Article
- Export citation
MTK volume 65 Issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 September 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
MTK volume 65 Issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 September 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation