Article contents
RANDOMNESS AND NON-RANDOMNESS PROPERTIES OF PIATETSKI-SHAPIRO SEQUENCES MODULO 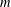 $m$
$m$
Published online by Cambridge University Press: 14 August 2019
Abstract
We study Piatetski-Shapiro sequences 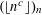 $(\lfloor n^{c}\rfloor )_{n}$ modulo
$(\lfloor n^{c}\rfloor )_{n}$ modulo 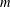 $m$, for non-integer
$m$, for non-integer 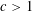 $c>1$ and positive
$c>1$ and positive 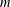 $m$, and we are particularly interested in subword occurrences in those sequences. We prove that each block
$m$, and we are particularly interested in subword occurrences in those sequences. We prove that each block 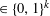 $\in \{0,1\}^{k}$ of length
$\in \{0,1\}^{k}$ of length 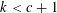 $k<c+1$ occurs as a subword with the frequency
$k<c+1$ occurs as a subword with the frequency 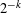 $2^{-k}$, while there are always blocks that do not occur. In particular, those sequences are not normal. For
$2^{-k}$, while there are always blocks that do not occur. In particular, those sequences are not normal. For 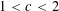 $1<c<2$, we estimate the number of subwords from above and below, yielding the fact that our sequences are deterministic and not morphic. Finally, using the Daboussi–Kátai criterion, we prove that the sequence
$1<c<2$, we estimate the number of subwords from above and below, yielding the fact that our sequences are deterministic and not morphic. Finally, using the Daboussi–Kátai criterion, we prove that the sequence 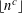 $\lfloor n^{c}\rfloor$ modulo
$\lfloor n^{c}\rfloor$ modulo 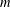 $m$ is asymptotically orthogonal to multiplicative functions bounded by 1 and with mean value 0.
$m$ is asymptotically orthogonal to multiplicative functions bounded by 1 and with mean value 0.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
Footnotes
This work was supported by the Austrian Science Foundation FWF, SFB F5502-N26 “Subsequences of Automatic Sequences and Uniform Distribution”, which is a part of the Special Research Program “Quasi Monte Carlo Methods: Theory and Applications”, by the joint ANR-FWF project ANR-14-CE34-0009, I-1751 MuDeRa, Ciência sem Fronteiras (project PVE 407308/2013-0) and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under the Grant Agreement No. 648132.
References
- 3
- Cited by


