Article contents
THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS
Published online by Cambridge University Press: 23 July 2019
Abstract
We consider sequences of the form 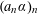 $(a_{n}\unicode[STIX]{x1D6FC})_{n}$ mod 1, where
$(a_{n}\unicode[STIX]{x1D6FC})_{n}$ mod 1, where 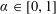 $\unicode[STIX]{x1D6FC}\in [0,1]$ and where
$\unicode[STIX]{x1D6FC}\in [0,1]$ and where 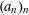 $(a_{n})_{n}$ is a strictly increasing sequence of positive integers. If the asymptotic distribution of the pair correlations of this sequence follows the Poissonian model for almost all
$(a_{n})_{n}$ is a strictly increasing sequence of positive integers. If the asymptotic distribution of the pair correlations of this sequence follows the Poissonian model for almost all  $\unicode[STIX]{x1D6FC}$ in the sense of Lebesgue measure, we say that
$\unicode[STIX]{x1D6FC}$ in the sense of Lebesgue measure, we say that 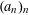 $(a_{n})_{n}$ has the metric pair correlation property. Recent research has revealed a connection between the metric theory of pair correlations of such sequences, and the additive energy of truncations of
$(a_{n})_{n}$ has the metric pair correlation property. Recent research has revealed a connection between the metric theory of pair correlations of such sequences, and the additive energy of truncations of 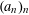 $(a_{n})_{n}$. Bloom, Chow, Gafni and Walker speculated that there might be a convergence/divergence criterion which fully characterizes the metric pair correlation property in terms of the additive energy, similar to Khintchine’s criterion in the metric theory of Diophantine approximation. In the present paper we give a negative answer to such speculations, by showing that such a criterion does not exist. To this end, we construct a sequence
$(a_{n})_{n}$. Bloom, Chow, Gafni and Walker speculated that there might be a convergence/divergence criterion which fully characterizes the metric pair correlation property in terms of the additive energy, similar to Khintchine’s criterion in the metric theory of Diophantine approximation. In the present paper we give a negative answer to such speculations, by showing that such a criterion does not exist. To this end, we construct a sequence 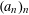 $(a_{n})_{n}$ having large additive energy which, however, maintains the metric pair correlation property.
$(a_{n})_{n}$ having large additive energy which, however, maintains the metric pair correlation property.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
References
- 8
- Cited by




