No CrossRef data available.
Article contents
INTERVALS BETWEEN CONSECUTIVE NUMBERS WHICH ARE SUMS OF TWO SQUARES
Published online by Cambridge University Press: 14 August 2019
Abstract
In this paper, we improve the moment estimates for the gaps between numbers that can be represented as a sum of two squares of integers. We consider a certain sum of Bessel functions and prove the upper bound for its mean value. This bound provides estimates for the 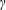 $\unicode[STIX]{x1D6FE}$th moments of gaps for all
$\unicode[STIX]{x1D6FE}$th moments of gaps for all 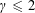 $\unicode[STIX]{x1D6FE}\leqslant 2$.
$\unicode[STIX]{x1D6FE}\leqslant 2$.
MSC classification
Secondary:
11B05: Density, gaps, topology
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2019
References
Bambah, R. P. and Chowla, S., On numbers which can be expressed as a sum of two squares. Proc. Nat. Acad. Sci. India
13
1947, 101–103.Google Scholar
Blomer, V. and Granville, A., Estimates for representation numbers of quadratic forms. Duke Math. J.
135(2) 2006, 261–302.10.1215/S0012-7094-06-13522-6Google Scholar
Cohen, H., Sums involving the values at negative integers of L-functions of quadratic characters. Math. Ann.
217
1975, 271–285.10.1007/BF01436180Google Scholar
Harman, G., Sums of two squares in short intervals. Proc. Lond. Math. Soc.
62
1991, 225–241.10.1112/plms/s3-62.2.225Google Scholar
Hooley, C., On the intervals between numbers that are sums of two squares I. Acta Math.
127
1971, 279–297.10.1007/BF02392056Google Scholar
Karatsuba, A. A., Euler and number theory. Proc. Steklov Inst. Math.
274(1) 2011, 169–179.10.1134/S0081543811070042Google Scholar
Kuznetsov, N. V., A new class of identities for the Fourier coefficients of modular forms. Acta Arith.
27
1975, 505–519 (in Russian).Google Scholar
Plaksin, V. A., The distribution of numbers representable as a sum of two squares. Izv. Akad. Nauk SSSR Ser. Mat.
51(4) 1987, 860–877. Engl. transl. Math. USSR-Izv.
31(1) (1988), 171–191.Google Scholar
Plaksin, V. A., Letter to the editor: correction to the paper “The distribution of numbers representable as a sum of two squares”. Izv. Math.
41(1) 1993, 187–188.10.1070/IM1993v041n01ABEH002256Google Scholar
Richards, I., On the gaps between numbers which are sums of two squares. Adv. Math.
46
1982, 1–2.10.1016/0001-8708(82)90051-2Google Scholar
Watson, G. N., A Treatise on the Theory of Bessel Functions, 2nd edn., Cambridge University Press (1966).Google Scholar




