Article contents
THE DUFFIN–SCHAEFFER-TYPE CONJECTURES IN VARIOUS LOCAL FIELDS
Published online by Cambridge University Press: 06 May 2016
Abstract
In this paper we study the Duffin–Schaeffer conjecture, which claims that 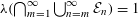 $\unicode[STIX]{x1D706}(\bigcap _{m=1}^{\infty }\bigcup _{n=m}^{\infty }{\mathcal{E}}_{n})=1$ if and only if
$\unicode[STIX]{x1D706}(\bigcap _{m=1}^{\infty }\bigcup _{n=m}^{\infty }{\mathcal{E}}_{n})=1$ if and only if 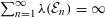 $\sum _{n=1}^{\infty }\unicode[STIX]{x1D706}({\mathcal{E}}_{n})=\infty$, where
$\sum _{n=1}^{\infty }\unicode[STIX]{x1D706}({\mathcal{E}}_{n})=\infty$, where  $\unicode[STIX]{x1D706}$ denotes the Lebesgue measure on
$\unicode[STIX]{x1D706}$ denotes the Lebesgue measure on 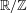 $\mathbb{R}/\mathbb{Z}$,
$\mathbb{R}/\mathbb{Z}$, 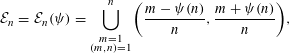 $$\begin{eqnarray}{\mathcal{E}}_{n}={\mathcal{E}}_{n}(\unicode[STIX]{x1D713})=\mathop{\bigcup }_{\substack{ m=1 \\ (m,n)=1}}^{n}\bigg(\frac{m-\unicode[STIX]{x1D713}(n)}{n},\frac{m+\unicode[STIX]{x1D713}(n)}{n}\bigg),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{n}={\mathcal{E}}_{n}(\unicode[STIX]{x1D713})=\mathop{\bigcup }_{\substack{ m=1 \\ (m,n)=1}}^{n}\bigg(\frac{m-\unicode[STIX]{x1D713}(n)}{n},\frac{m+\unicode[STIX]{x1D713}(n)}{n}\bigg),\end{eqnarray}$$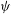 $\unicode[STIX]{x1D713}$ denotes any non-negative arithmetical function. Instead of studying the superior limit
$\unicode[STIX]{x1D713}$ denotes any non-negative arithmetical function. Instead of studying the superior limit 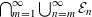 $\bigcap _{m=1}^{\infty }\bigcup _{n=m}^{\infty }{\mathcal{E}}_{n}$ we focus on the union
$\bigcap _{m=1}^{\infty }\bigcup _{n=m}^{\infty }{\mathcal{E}}_{n}$ we focus on the union 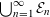 $\bigcup _{n=1}^{\infty }{\mathcal{E}}_{n}$ and conjecture that there exists a universal constant
$\bigcup _{n=1}^{\infty }{\mathcal{E}}_{n}$ and conjecture that there exists a universal constant 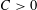 $C>0$ such that
$C>0$ such that 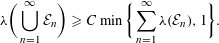 $$\begin{eqnarray}\unicode[STIX]{x1D706}\bigg(\mathop{\bigcup }_{n=1}^{\infty }{\mathcal{E}}_{n}\bigg)\geqslant C\min \bigg\{\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D706}({\mathcal{E}}_{n}),1\bigg\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}\bigg(\mathop{\bigcup }_{n=1}^{\infty }{\mathcal{E}}_{n}\bigg)\geqslant C\min \bigg\{\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D706}({\mathcal{E}}_{n}),1\bigg\}.\end{eqnarray}$$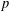 $p$-adic numbers and formal Laurent series. Furthermore, two conjectures of Haynes, Pollington and Velani are shown to be equivalent to the Duffin–Schaeffer conjecture, and a weighted version of the second Borel–Cantelli lemma is introduced to study the Duffin–Schaeffer conjecture.
$p$-adic numbers and formal Laurent series. Furthermore, two conjectures of Haynes, Pollington and Velani are shown to be equivalent to the Duffin–Schaeffer conjecture, and a weighted version of the second Borel–Cantelli lemma is introduced to study the Duffin–Schaeffer conjecture.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 1
- Cited by




