Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Manoussakis, Antonis
Pelczar-Barwacz, Anna
and
Świȩtek, Michał
2017.
An unconditionally saturated Banach space with the scalar-plus-compact property.
Journal of Functional Analysis,
Vol. 272,
Issue. 12,
p.
4944.
Godefroy, Gilles
and
Saint-Raymond, Jean
2018.
Descriptive complexity of some isomorphism classes of Banach spaces.
Journal of Functional Analysis,
Vol. 275,
Issue. 4,
p.
1008.
Kurka, Ondřej
2018.
Tsirelson-like spaces and complexity of classes of Banach spaces.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 112,
Issue. 4,
p.
1101.
Kurka, Ondřej
2019.
The isomorphism class of C0 is not Borel.
Israel Journal of Mathematics,
Vol. 231,
Issue. 1,
p.
243.
CAUSEY, RYAN MICHAEL
2020.
CONCERNING SUMMABLE SZLENK INDEX.
Glasgow Mathematical Journal,
Vol. 62,
Issue. 1,
p.
59.
Causey, R.
Fovelle, A.
and
Lancien, G.
2022.
Asymptotic smoothness in Banach spaces, three-space properties and applications.
Transactions of the American Mathematical Society,
Vol. 376,
Issue. 3,
p.
1895.
Hájek, Petr
and
Medina, Rubén
2023.
Schauder bases in Lipschitz free spaces over nets of $${\mathcal {L}}_{\infty }$$-spaces.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 117,
Issue. 1,
Motakis, Pavlos
2023.
Separable spaces of continuous functions as Calkin algebras.
Journal of the American Mathematical Society,
Vol. 37,
Issue. 1,
p.
1.
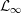 ${\mathcal{L}}_{\infty }$-SPACES
${\mathcal{L}}_{\infty }$-SPACES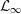 ${\mathcal{L}}_{\infty }$-space is isomorphic to such a space. Furthermore, we provide an example of a
${\mathcal{L}}_{\infty }$-space is isomorphic to such a space. Furthermore, we provide an example of a 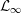 ${\mathcal{L}}_{\infty }$ and asymptotic
${\mathcal{L}}_{\infty }$ and asymptotic 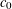 $c_{0}$ space not containing
$c_{0}$ space not containing 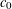 $c_{0}$.
$c_{0}$.

