Article contents
ON SUMS OF FOUR SQUARES OF PRIMES
Published online by Cambridge University Press: 22 January 2016
Abstract
Let 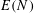 $E(N)$ denote the number of positive integers
$E(N)$ denote the number of positive integers 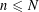 $n\leqslant N$, with
$n\leqslant N$, with  $n\equiv 4\;(\text{mod}\;24)$, which cannot be represented as the sum of four squares of primes. We establish that
$n\equiv 4\;(\text{mod}\;24)$, which cannot be represented as the sum of four squares of primes. We establish that 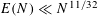 $E(N)\ll N^{11/32}$, thus improving on an earlier result of Harman and the first author, where the exponent
$E(N)\ll N^{11/32}$, thus improving on an earlier result of Harman and the first author, where the exponent 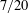 $7/20$ appears in place of
$7/20$ appears in place of 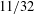 $11/32$.
$11/32$.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 4
- Cited by




