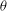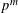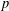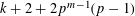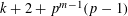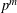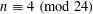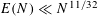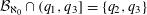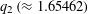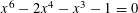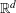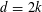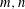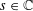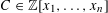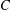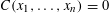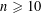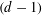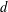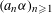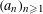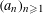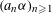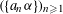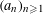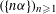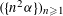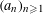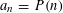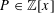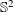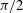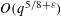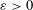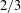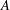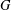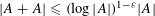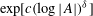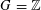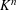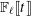Research Article
ON THE THETA OPERATOR FOR MODULAR FORMS MODULO PRIME POWERS
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 321-336
-
- Article
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
-
- Article
- Export citation
ON SUMS OF FOUR SQUARES OF PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 348-361
-
- Article
- Export citation
ON SMALL BASES FOR WHICH 1 HAS COUNTABLY MANY EXPANSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 362-377
-
- Article
- Export citation
DECOMPOSITION OF BALLS IN
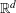 $\mathbb{R}^{d}$
$\mathbb{R}^{d}$
- Part of:
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 378-405
-
- Article
- Export citation
OPPOSITE-SIGN KLOOSTERMAN SUM ZETA FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2016, pp. 406-429
-
- Article
- Export citation
RATIONAL POINTS ON CUBIC HYPERSURFACES THAT SPLIT INTO FOUR FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2016, pp. 430-440
-
- Article
- Export citation
LOWER BOUND THEOREMS AND A GENERALIZED LOWER BOUND CONJECTURE FOR BALANCED SIMPLICIAL COMPLEXES
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2016, pp. 441-477
-
- Article
- Export citation
METRIC RESULTS ON THE DISCREPANCY OF SEQUENCES
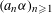 $(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES
$(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES 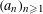 $(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH
$(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2016, pp. 478-491
-
- Article
- Export citation
ORTHOGONAL COLORINGS OF THE SPHERE
- Part of:
-
- Published online by Cambridge University Press:
- 04 February 2016, pp. 492-501
-
- Article
- Export citation
BIG BIASES AMONGST PRODUCTS OF TWO PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2016, pp. 502-507
-
- Article
- Export citation
EXPONENTIAL SUMS OVER PRIMES IN SHORT INTERVALS AND AN APPLICATION TO THE WARING–GOLDBACH PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 508-523
-
- Article
- Export citation
WARING’S PROBLEM WITH PIATETSKI-SHAPIRO NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 524-550
-
- Article
- Export citation
SMALL SOLUTIONS OF QUADRATIC CONGRUENCES, AND CHARACTER SUMS WITH BINARY QUADRATIC FORMS
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2016, pp. 551-571
-
- Article
- Export citation
PRIMES IN BEATTY SEQUENCES IN SHORT INTERVALS
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 572-586
-
- Article
- Export citation
ARITHMETIC PROGRESSIONS IN SETS OF SMALL DOUBLING
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 587-613
-
- Article
- Export citation
KAKEYA-TYPE SETS IN LOCAL FIELDS WITH FINITE RESIDUE FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 614-629
-
- Article
- Export citation
A SPIKY BALL
- Part of:
-
- Published online by Cambridge University Press:
- 17 February 2016, pp. 630-636
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK volume 62 Issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 28 April 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
MTK volume 62 Issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 28 April 2016, pp. b1-b6
-
- Article
-
- You have access
- Export citation