Article contents
ON THE THETA OPERATOR FOR MODULAR FORMS MODULO PRIME POWERS
Published online by Cambridge University Press: 22 January 2016
Abstract
We consider the classical theta operator 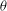 ${\it\theta}$ on modular forms modulo
${\it\theta}$ on modular forms modulo 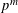 $p^{m}$ and level
$p^{m}$ and level 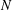 $N$ prime to
$N$ prime to 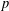 $p$, where
$p$, where 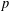 $p$ is a prime greater than three. Our main result is that
$p$ is a prime greater than three. Our main result is that 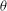 ${\it\theta}$ mod
${\it\theta}$ mod 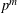 $p^{m}$ will map forms of weight
$p^{m}$ will map forms of weight 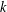 $k$ to forms of weight
$k$ to forms of weight 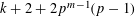 $k+2+2p^{m-1}(p-1)$ and that this weight is optimal in certain cases when
$k+2+2p^{m-1}(p-1)$ and that this weight is optimal in certain cases when 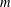 $m$ is at least two. Thus, the natural expectation that
$m$ is at least two. Thus, the natural expectation that 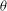 ${\it\theta}$ mod
${\it\theta}$ mod 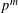 $p^{m}$ should map to weight
$p^{m}$ should map to weight 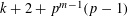 $k+2+p^{m-1}(p-1)$ is shown to be false. The primary motivation for this study is that application of the
$k+2+p^{m-1}(p-1)$ is shown to be false. The primary motivation for this study is that application of the 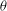 ${\it\theta}$ operator on eigenforms mod
${\it\theta}$ operator on eigenforms mod 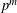 $p^{m}$ corresponds to twisting the attached Galois representations with the cyclotomic character. Our construction of the
$p^{m}$ corresponds to twisting the attached Galois representations with the cyclotomic character. Our construction of the 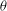 ${\it\theta}$-operator mod
${\it\theta}$-operator mod 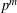 $p^{m}$ gives an explicit weight bound on the twist of a modular mod
$p^{m}$ gives an explicit weight bound on the twist of a modular mod 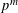 $p^{m}$ Galois representation by the cyclotomic character.
$p^{m}$ Galois representation by the cyclotomic character.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 3
- Cited by




