Article contents
SOME SHARP BILINEAR SPACE–TIME ESTIMATES FOR THE WAVE EQUATION
Published online by Cambridge University Press: 07 March 2016
Abstract
We prove a family of sharp bilinear space–time estimates for the half-wave propagator 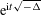 $\text{e}^{\text{i}t\sqrt{-\unicode[STIX]{x1D6E5}}}$. As a consequence, for radially symmetric initial data, we establish sharp estimates of this kind for a range of exponents beyond the classical range.
$\text{e}^{\text{i}t\sqrt{-\unicode[STIX]{x1D6E5}}}$. As a consequence, for radially symmetric initial data, we establish sharp estimates of this kind for a range of exponents beyond the classical range.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 4
- Cited by


