Article contents
UNIONS OF LINES IN 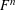 $F^{n}$
$F^{n}$
Published online by Cambridge University Press: 11 April 2016
Abstract
We show that if a collection of lines in a vector space over a finite field has “dimension” at least 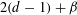 $2(d-1)+\unicode[STIX]{x1D6FD}$, then its union has “dimension” at least
$2(d-1)+\unicode[STIX]{x1D6FD}$, then its union has “dimension” at least 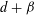 $d+\unicode[STIX]{x1D6FD}$. This is the sharp estimate of its type when no structural assumptions are placed on the collection of lines. We also consider some refinements and extensions of the main result, including estimates for unions of
$d+\unicode[STIX]{x1D6FD}$. This is the sharp estimate of its type when no structural assumptions are placed on the collection of lines. We also consider some refinements and extensions of the main result, including estimates for unions of 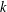 $k$-planes.
$k$-planes.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2016
References
- 2
- Cited by




