Analyzing Sequential Categorical Data: Individual Variation in Markov Chains
-
- Journal:
- Psychometrika / Volume 55 / Issue 2 / June 1990
- Published online by Cambridge University Press:
- 01 January 2025, pp. 263-275
-
- Article
- Export citation
Estimation of the Nonlinear Random Coefficient Model when Some Random Effects Are Separable
-
- Journal:
- Psychometrika / Volume 74 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 January 2025, pp. 65-82
-
- Article
- Export citation
High-dimensional Exploratory Item Factor Analysis by A Metropolis–Hastings Robbins–Monro Algorithm
-
- Journal:
- Psychometrika / Volume 75 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 January 2025, pp. 33-57
-
- Article
-
- You have access
- Open access
- Export citation
Integration of the modified double layer potential of the vector boundary element method for eddy current problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 16 June 2022, pp. 385-407
-
- Article
- Export citation
CONFIDENCE INTERVALS IN GENERAL REGRESSION MODELS THAT UTILISE UNCERTAIN PRIOR INFORMATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 516-517
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
9 - Simulation Methods
-
- Book:
- Structural and System Reliability
- Published online:
- 13 January 2022
- Print publication:
- 13 January 2022, pp 262-300
-
- Chapter
- Export citation
ALGORITHM TO CONSTRUCT INTEGRO SPLINES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 3 / July 2021
- Published online by Cambridge University Press:
- 13 September 2021, pp. 359-375
-
- Article
- Export citation
7 - Mapping, Shape Functions, and Numerical Integration
-
- Book:
- Finite Element Method for Solids and Structures
- Published online:
- 08 July 2021
- Print publication:
- 17 June 2021, pp 184-215
-
- Chapter
- Export citation
Asymptotic variance of Newton–Cotes quadratures based on randomized sampling points
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1284-1307
- Print publication:
- December 2020
-
- Article
- Export citation
3 - Numerical Analysis Methods
-
- Book:
- Introduction to the Finite Element Method and Implementation with MATLAB®
- Published online:
- 09 December 2020
- Print publication:
- 30 July 2020, pp 52-83
-
- Chapter
- Export citation
B - Numerical techniques
-
- Book:
- Actuarial Mathematics for Life Contingent Risks
- Published online:
- 30 April 2020
- Print publication:
- 19 December 2019, pp 727-731
-
- Chapter
- Export citation
11 - Numerical modeling
-
- Book:
- Principles of Glacier Mechanics
- Published online:
- 20 December 2019
- Print publication:
- 05 December 2019, pp 291-319
-
- Chapter
- Export citation
5 - Calculus
-
- Book:
- The Student's Introduction to <I>Mathematica</I> and the Wolfram Language
- Published online:
- 01 April 2019
- Print publication:
- 16 May 2019, pp 191-248
-
- Chapter
- Export citation
Energy Supplementation Strategies for Wheat Pasture Stocker Cattle Under Uncertain Forage Availability
-
- Journal:
- Journal of Agricultural and Applied Economics / Volume 28 / Issue 1 / July 1996
- Published online by Cambridge University Press:
- 28 April 2015, pp. 172-179
-
- Article
- Export citation
Measuring the Irreversibility of Numerical Schemes forReversible Stochastic Differential Equations∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 48 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 13 August 2014, pp. 1351-1379
- Print publication:
- September 2014
-
- Article
- Export citation
Simple Fourth-Degree Cubature Formulae with Few Nodes over General Product Regions
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 7 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 179-192
- Print publication:
- May 2014
-
- Article
- Export citation
A Frequency Determination Method for Digitized NMR Signals
-
- Journal:
- Communications in Computational Physics / Volume 15 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1343-1351
- Print publication:
- May 2014
-
- Article
- Export citation
A Matrix-Vector Operation-Based Numerical Solution Method for Linear m-th Order Ordinary Differential Equations: Application to Engineering Problems
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 5 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 269-308
- Print publication:
- June 2013
-
- Article
- Export citation
A simple damage-gradient enhanced elastoplastic formulation andits numerical implementation
-
- Journal:
- Mechanics & Industry / Volume 13 / Issue 2 / 2012
- Published online by Cambridge University Press:
- 18 July 2012, pp. 97-110
- Print publication:
- 2012
-
- Article
- Export citation
Exponential convergence of hp quadraturefor integral operators with Gevrey kernels
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 45 / Issue 3 / May 2011
- Published online by Cambridge University Press:
- 11 October 2010, pp. 387-422
- Print publication:
- May 2011
-
- Article
- Export citation

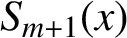
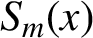
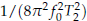 if the observation time
if the observation time 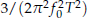 which is one order more precise than the ±1 count error induced precision of a typical frequency counter. Analysis of this method shows that the integration reduces the noise by bandwidth narrowing as in a lock-in amplifier, and no extra signal filters are needed. For a pure sinusoidal signal we find from numerical simulations that the noise-induced error in this method reaches the Cramer-Rao Lower Band (CRLB) on frequency determination. For the damped sinusoidal case of most interest, the noise-induced error is found to be within a factor of 2 of CRLB when the measurement time
which is one order more precise than the ±1 count error induced precision of a typical frequency counter. Analysis of this method shows that the integration reduces the noise by bandwidth narrowing as in a lock-in amplifier, and no extra signal filters are needed. For a pure sinusoidal signal we find from numerical simulations that the noise-induced error in this method reaches the Cramer-Rao Lower Band (CRLB) on frequency determination. For the damped sinusoidal case of most interest, the noise-induced error is found to be within a factor of 2 of CRLB when the measurement time