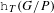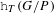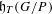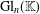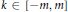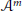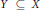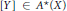23 results
Pebble trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hilbert series of the superspace coinvariant ring
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 17 October 2024, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Derived categories of skew-gentle algebras and orbifolds
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 31 January 2022, pp. 649-674
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERACTING QUARTER-PLANE LATTICE WALK PROBLEMS: SOLUTIONS AND PROOFS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 05 November 2021, pp. 339-340
- Print publication:
- April 2022
-
- Article
-
- You have access
- HTML
- Export citation
Additive bases via Fourier analysis
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 930-941
-
- Article
- Export citation
FRIEZE PATTERNS WITH COEFFICIENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 March 2020, e17
-
- Article
-
- You have access
- Open access
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
GRASSMANNIAN SEMIGROUPS AND THEIR REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 27 March 2018, pp. 308-337
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
A probabilistic interpretation of the Gaussian binomial coefficients
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1295-1298
- Print publication:
- December 2017
-
- Article
- Export citation
One-dimensional Schubert Problems with Respect to Osculating Flags
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 1 / 01 February 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 143-185
- Print publication:
- 01 February 2017
-
- Article
-
- You have access
- Export citation
Weighted Random Staircase Tableaux
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 6 / November 2014
- Published online by Cambridge University Press:
- 15 July 2014, pp. 1114-1147
-
- Article
- Export citation
On the k-Buchsbaum property of powers of Stanley–Reisner ideals
-
- Journal:
- Nagoya Mathematical Journal / Volume 213 / March 2014
- Published online by Cambridge University Press:
- 11 January 2016, pp. 127-140
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Lagrange's Theorem for Hopf Monoids in Species
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 2 / 01 April 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-265
- Print publication:
- 01 April 2013
-
- Article
-
- You have access
- Export citation
Note on Cubature Formulae and Designs Obtained from Group Orbits
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 6 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1359-1377
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
Proof of a positivity conjecture of M. Kontsevich on non-commutative cluster variables
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 31 October 2012, pp. 1821-1832
- Print publication:
- November 2012
-
- Article
-
- You have access
- Export citation
Recurrence Relations for Strongly q-Log-Convex Polynomials
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 2 / 01 June 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 217-229
- Print publication:
- 01 June 2011
-
- Article
-
- You have access
- Export citation
A Combinatorial Reciprocity Theorem for Hyperplane Arrangements
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 1 / 01 March 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-10
- Print publication:
- 01 March 2010
-
- Article
-
- You have access
- Export citation
Multiplicity-Free Schubert Calculus
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 1 / 01 March 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 171-186
- Print publication:
- 01 March 2010
-
- Article
-
- You have access
- Export citation
On Canonical Modules of Toric Face Rings
-
- Journal:
- Nagoya Mathematical Journal / Volume 194 / 2009
- Published online by Cambridge University Press:
- 11 January 2016, pp. 69-90
- Print publication:
- 2009
-
- Article
-
- You have access
- Export citation
Small resolutions of minuscule Schubert varieties
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 5 / September 2007
- Published online by Cambridge University Press:
- 20 September 2007, pp. 1255-1312
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation