Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-22T11:49:42.590Z Has data issue: false hasContentIssue false
  • English
  • Français

A Combinatorial Reciprocity Theorem for Hyperplane Arrangements

Published online by Cambridge University Press:  20 November 2018

Christos A. Athanasiadis
Christos A. Athanasiadis*
Affiliation:
Department of Mathematics (Division of Algebra-Geometry), University of Athens, Panepistimioupolis, 15784 Athens, Greece e-mail: caath@math.uoa.gr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a nonnegative integer 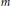$m$ and a finite collection 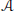$A$ of linear forms on 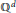${{\mathbb{Q}}^{d}}$, the arrangement of affine hyperplanes in 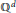${{\mathbb{Q}}^{d}}$ defined by the equations 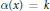$\alpha \left( x \right)\,=\,k$ for 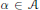$\alpha \,\in \,A$ and integers 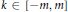$k\,\in \,\left[ -m,\,m \right]$ is denoted by 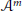${{A}^{m}}$. It is proved that the coefficients of the characteristic polynomial of 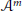${{A}^{m}}$ are quasi-polynomials in 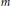$m$ and that they satisfy a simple combinatorial reciprocity law.

Keywords

52C3505E99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 1 , 01 March 2010 , pp. 3 - 10
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Athanasiadis, C. A., Deformations of Coxeter hyperplane arrangements and their characteristic polynomials. In: Arrangements—Tokyo 1998, Adv. Stud. Pure Math. 27, Kinokuniya, Tokyo, 2000, pp. 1–26.Google Scholar
[2] Athanasiadis, C. A., Generalized Catalan numbers, Weyl groups and arrangements of hyperplanes. Bull. London Math. Soc. 36(2004), no. 3, 294–302. doi:10.1112/S0024609303002856Google Scholar
[3] Athanasiadis, C. A. and Tzanaki, E., On the enumeration of positive cells in generalized cluster complexes and Catalan hyperplane arrangements. J. Algebraic Combin. 23(2006), no. 4, 355–375. doi:10.1007/s10801-006-8348-8Google Scholar
[4] Björner, A. and Brenti, F., Combinatorics of Coxeter groups. Graduate Texts in Mathematics 231, Springer, New York, 2005.Google Scholar
[5] Bourbaki, N., Lie groups and Lie algebras. Chapters 4–6, Springer-Verlag, Berlin, 2002.Google Scholar
[6] Fomin, S. and Reading, N., Generalized cluster complexes and Coxeter combinatorics. Int. Math. Res. Not. 2005, no. 44, 2709–2757.Google Scholar
[7] Humphreys, J. E., Reflection groups and Coxeter groups. Cambridge Studies in Advanced Mathematics 29, Cambridge University Press, Cambridge, 1990.Google Scholar
[8] Orlik, P. and Solomon, L., Combinatorics and topology of complements of hyperplanes. Invent. Math. 56(1980), no. 2, 167–189. doi:10.1007/BF01392549Google Scholar
[9] Orlik, P. and Terao, H., Arrangements of hyperplanes. Grundlehren der Mathematischen Wissenschaften 300, Springer-Verlag, Berlin, 1992.Google Scholar
[10] Postnikov, A. and Stanley, R. P., Deformations of Coxeter hyperplane arrangements. J. Combin. Theory Series A 91(2000), no. 1–2, 544–597. doi:10.1006/jcta.2000.3106Google Scholar
[11] Stanley, R. P., Combinatorial reciprocity theorems. Advances in Math. 14(1974), 194–253. doi:10.1016/0001-8708(74)90030-9Google Scholar
[12] Stanley, R. P., Enumerative Combinatorics Vol. 1. Cambridge Studies in Advanced Mathematics 49, Cambridge University Press, Cambridge, 1997.Google Scholar
[13] Stanley, R. P., An Introduction to hyperplane arrangements. In: Geometric combinatorics, IAS/Park City Math. Ser. 13, American Mathematical Society, Providence, RI, 2007.Google Scholar
[14] Zaslavsky, T., Facing up to arrangements: face-count formulas for partitions of space by hyperplanes. Mem. Amer. Math. Soc. 1(1975), no. 154.Google Scholar