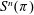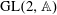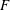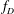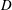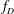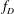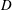Research Article
Level-raising and symmetric power functoriality, I
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 729-748
-
- Article
-
- You have access
- Export citation
On a completed generating function of locally harmonic Maass forms
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 749-762
-
- Article
-
- You have access
- Export citation
Strong orthogonality between the Möbius function, additive characters and Fourier coefficients of cusp forms
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2014, pp. 763-797
-
- Article
-
- You have access
- Export citation
Ramification theory and perfectoid spaces
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2014, pp. 798-834
-
- Article
-
- You have access
- Export citation
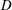 $D$-modules on spaces of rational maps
$D$-modules on spaces of rational maps
- Part of:
-
- Published online by Cambridge University Press:
- 31 March 2014, pp. 835-876
-
- Article
-
- You have access
- Export citation
On the homomorphisms between scalar generalized Verma modules
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2014, pp. 877-892
-
- Article
-
- You have access
- Export citation
A generalization of Ohkawa’s theorem
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2014, pp. 893-902
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 150 Issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 23 May 2014, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
COM volume 150 Issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 23 May 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation