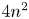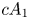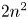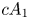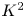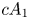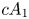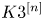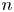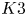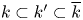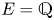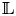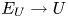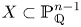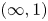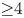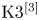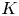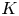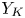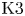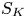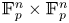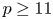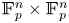Open access
Research Article
2 n2-inequality for cA1 points and applications to birational rigidity
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1551-1595
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thin links and Conway spheres
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1467-1524
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of:
-
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational Hodge isometries of hyper-Kähler varieties of
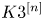 $K3^{[n]}$ type are algebraic
$K3^{[n]}$ type are algebraic
- Part of:
-
- Published online by Cambridge University Press:
- 07 May 2024, pp. 1261-1303
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral decomposition of genuine cusp forms over global function fields
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1194-1260
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Fields of moduli and the arithmetic of tame quotient singularities
- Part of:
-
- Published online by Cambridge University Press:
- 27 March 2024, pp. 982-1003
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modular curves and Néron models of generalized Jacobians
- Part of:
-
- Published online by Cambridge University Press:
- 26 March 2024, pp. 945-981
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convexity of multiplicities of filtrations on local rings
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2024, pp. 878-914
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Constructing abelian varieties from rank 2 Galois representations
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2024, pp. 709-731
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hasse principle for complete intersections
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 771-835
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On straightening for Segal spaces
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2024, pp. 586-656
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stratification of the transverse momentum map
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2024, pp. 518-585
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boundedness of the p-primary torsion of the Brauer group of an abelian variety
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2024, pp. 463-480
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isoparametric hypersurfaces in symmetric spaces of non-compact type and higher rank
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2024, pp. 451-462
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sixfolds of generalized Kummer type and K3 surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2024, pp. 388-410
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher semiadditive algebraic K-theory and redshift
- Part of:
-
- Published online by Cambridge University Press:
- 15 December 2023, pp. 237-287
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subsets of
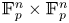 $\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
$\mathbb {F}_p^n\times \mathbb {F}_p^n$ without L-shaped configurations
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2023, pp. 176-236
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite orbits for large groups of automorphisms of projective surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 30 November 2023, pp. 120-175
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On equivariant topological modular forms
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2023, pp. 2638-2693
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Locality of relative symplectic cohomology for complete embeddings
- Part of:
-
- Published online by Cambridge University Press:
- 10 October 2023, pp. 2551-2637
-
- Article
-
- You have access
- Open access
- HTML
- Export citation