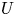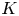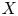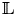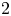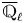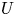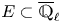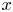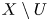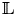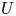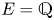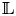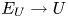1. Introduction
To state our main result, we require the following definition and setup.
Definition 1.1 Let ![]() $B/k$ be a smooth variety over a finitely generated field and let
$B/k$ be a smooth variety over a finitely generated field and let ![]() $\ell \neq \text {char}(k)$ be a prime. An abelian scheme
$\ell \neq \text {char}(k)$ be a prime. An abelian scheme ![]() $g\colon A_B\rightarrow B$ is said to be of
$g\colon A_B\rightarrow B$ is said to be of ![]() ${\rm SL}_2$-type if there is a decomposition of lisse
${\rm SL}_2$-type if there is a decomposition of lisse ![]() $\overline {\mathbb {Q}}_{\ell }$-sheaves on
$\overline {\mathbb {Q}}_{\ell }$-sheaves on ![]() $B$:
$B$:
where each ![]() ${\mathbb {L}}_i$ is a geometrically irreducible rank
${\mathbb {L}}_i$ is a geometrically irreducible rank ![]() $2$ lisse
$2$ lisse ![]() $\overline {\mathbb {Q}}_{\ell }$-sheaf on
$\overline {\mathbb {Q}}_{\ell }$-sheaf on ![]() $B$ with cyclotomic determinant
$B$ with cyclotomic determinant ![]() $\bigwedge ^2{\mathbb {L}}_i\cong {\overline {{\mathbb {Q}}}_\ell }(1)$.
$\bigwedge ^2{\mathbb {L}}_i\cong {\overline {{\mathbb {Q}}}_\ell }(1)$.
Setup 1.2 Let ![]() $K$ be a number field and let
$K$ be a number field and let ![]() $X/K$ be a smooth, proper, geometrically irreducible curve. Let
$X/K$ be a smooth, proper, geometrically irreducible curve. Let ![]() $U\subset X$ be a Zariski open and dense subset of
$U\subset X$ be a Zariski open and dense subset of ![]() $X$ with reduced complementary divisor
$X$ with reduced complementary divisor ![]() $D$. Assume that
$D$. Assume that ![]() $D$ is non-empty.
$D$ is non-empty.
Let ![]() $f\colon A_U\rightarrow U$ be a generically simple abelian scheme that is of
$f\colon A_U\rightarrow U$ be a generically simple abelian scheme that is of ![]() $\mathrm {SL}_2$-type and has bad, infinite reduction along some non-empty subset of
$\mathrm {SL}_2$-type and has bad, infinite reduction along some non-empty subset of ![]() $D$. Then the following statements hold for each direct summand
$D$. Then the following statements hold for each direct summand ![]() ${\mathbb {L}}_i$ of
${\mathbb {L}}_i$ of ![]() $R^1f_{*}\overline {\mathbb {Q}}_{\ell }$.
$R^1f_{*}\overline {\mathbb {Q}}_{\ell }$.
(1) The summand
 ${\mathbb {L}}_i$ is a geometrically irreducible, rank 2 lisse
${\mathbb {L}}_i$ is a geometrically irreducible, rank 2 lisse  $\overline {\mathbb {Q}}_{\ell }$-sheaf on
$\overline {\mathbb {Q}}_{\ell }$-sheaf on  $U$ with cyclotomic determinant:
$U$ with cyclotomic determinant:  $\bigwedge ^2{\mathbb {L}}_i\cong {\overline {{\mathbb {Q}}}_\ell }(1)$.
$\bigwedge ^2{\mathbb {L}}_i\cong {\overline {{\mathbb {Q}}}_\ell }(1)$.(2) There exists a proper smooth model
 ${\mathfrak {X}}$ over
${\mathfrak {X}}$ over  ${\mathcal {O}_K[1/N]}$, an open subset
${\mathcal {O}_K[1/N]}$, an open subset  ${\mathfrak {U}}$ of
${\mathfrak {U}}$ of  ${\mathfrak {X}}$ extending
${\mathfrak {X}}$ extending  $U$, an
$U$, an  $\ell$-adic local field
$\ell$-adic local field  $M$, and a lisse
$M$, and a lisse  $\mathcal {O}_M$-sheaf
$\mathcal {O}_M$-sheaf  ${\mathcal {L}}_i$ on
${\mathcal {L}}_i$ on  ${\mathfrak {U}}$ such that
${\mathfrak {U}}$ such that
 \[ ({\mathcal{L}}_i\otimes_{\mathcal{O}_M}\overline{\mathbb{Q}}_{\ell})|_{U} \cong {\mathbb{L}}_i. \]
\[ ({\mathcal{L}}_i\otimes_{\mathcal{O}_M}\overline{\mathbb{Q}}_{\ell})|_{U} \cong {\mathbb{L}}_i. \]
(3) There exists a number field
 $E$ such that for each closed point
$E$ such that for each closed point  $x$ of
$x$ of  ${\mathfrak {U}}$, the trace of Frobenius on
${\mathfrak {U}}$, the trace of Frobenius on  $({\mathcal {L}}_i)_x$ is in
$({\mathcal {L}}_i)_x$ is in  $E\subset \overline {\mathbb {Q}}_{\ell }$.
$E\subset \overline {\mathbb {Q}}_{\ell }$.(4) The local (geometric) monodromy of
 ${\mathbb {L}}_i$ is infinite around some non-empty subset of
${\mathbb {L}}_i$ is infinite around some non-empty subset of  $D$.
$D$.
In [Reference Snowden and TsimermanST18], Snowden and Tsimerman prove that when ![]() $E={\mathbb {Q}}$, the above four conditions characterize those lisse
$E={\mathbb {Q}}$, the above four conditions characterize those lisse ![]() $\overline {\mathbb {Q}}_{\ell }$-sheaves coming from families of elliptic curves. More precisely, they prove the following.
$\overline {\mathbb {Q}}_{\ell }$-sheaves coming from families of elliptic curves. More precisely, they prove the following.
Theorem 1.3 (Snowden–Tsimerman)
Let the notation be as in Setup 1.2 and let ![]() ${\mathbb {L}}$ be a lisse
${\mathbb {L}}$ be a lisse ![]() $\overline {\mathbb {Q}}_{\ell }$-sheaf on
$\overline {\mathbb {Q}}_{\ell }$-sheaf on ![]() $U$ satisfying the above conditions (1)–(4), with
$U$ satisfying the above conditions (1)–(4), with ![]() $E={\mathbb {Q}}$. Then there exists a family of elliptic curves
$E={\mathbb {Q}}$. Then there exists a family of elliptic curves
and an isomorphism ![]() ${\mathbb {L}} \cong {\rm R}^1f_*({\overline {{\mathbb {Q}}}_\ell })$.
${\mathbb {L}} \cong {\rm R}^1f_*({\overline {{\mathbb {Q}}}_\ell })$.
In this article, we consider the situation where Frobenius traces are all contained in a fixed number field ![]() $E$.
$E$.
Theorem 1.4 Let the notation be as in Setup 1.2 and let ![]() ${\mathbb {L}}$ be a lisse
${\mathbb {L}}$ be a lisse ![]() $\overline {\mathbb {Q}}_{\ell }$-sheaf on
$\overline {\mathbb {Q}}_{\ell }$-sheaf on ![]() $U$ satisfying conditions (1)–(4). Then there exists an abelian scheme
$U$ satisfying conditions (1)–(4). Then there exists an abelian scheme
such that ![]() ${\mathbb {L}}$ is a summand
${\mathbb {L}}$ is a summand ![]() $\mathrm {R}^1f_*({\overline {{\mathbb {Q}}}_\ell })$.
$\mathrm {R}^1f_*({\overline {{\mathbb {Q}}}_\ell })$.
Remark 1.5 We view Theorem 1.4 as providing a bit of further evidence for the relative Fontaine–Mazur conjecture, as in [Reference Liu and ZhuLZ17, Conjecture, p. 292] or [Reference PetrovPet23, Conjecture 1].
An observation of Litt implies that for an arithmetic local system, condition (2) will automatically hold: see step 2 of the proof of [Reference LittLit21, Theorem 1.1.3] or [Reference PetrovPet23, Theorem 6.1]. (See also the argument in [Reference Liu and ZhuLZ17, Proposition 4.1].) Therefore, to prove the relative Fontaine–Mazur conjecture for rank ![]() $2$ local systems that have infinite monodromy around some point, it suffices to bound the field generated by Frobenius traces. This task seems to be quite difficult in general; for some progress on this question, see [Reference ShimizuShi20].
$2$ local systems that have infinite monodromy around some point, it suffices to bound the field generated by Frobenius traces. This task seems to be quite difficult in general; for some progress on this question, see [Reference ShimizuShi20].
Remark 1.6 We do not have any idea how to get around point (4). As will be explained in the proof sketch, this is because we crucially use some of Drinfeld's early work on the Langlands correspondence for ![]() $\text {GL}_2$ over function fields. More specifically, he is able to show that if
$\text {GL}_2$ over function fields. More specifically, he is able to show that if ![]() ${\mathbb {L}}$ is an irreducible rank 2 lisse
${\mathbb {L}}$ is an irreducible rank 2 lisse ![]() $\overline {\mathbb {Q}}_{\ell }$-sheaf over a curve
$\overline {\mathbb {Q}}_{\ell }$-sheaf over a curve ![]() $U/\mathbb {F}_q$ with cyclotomic determinant and infinite monodromy at
$U/\mathbb {F}_q$ with cyclotomic determinant and infinite monodromy at ![]() $\infty$, then
$\infty$, then ![]() ${\mathbb {L}}$ comes from a family of abelian varieties over
${\mathbb {L}}$ comes from a family of abelian varieties over ![]() $U$. His proof finds such an abelian scheme as an isogeny factor of a Drinfeld modular curve over
$U$. His proof finds such an abelian scheme as an isogeny factor of a Drinfeld modular curve over ![]() $\mathbb {F}_q(U)$.Footnote 1 When we do not assume infinite monodromy at
$\mathbb {F}_q(U)$.Footnote 1 When we do not assume infinite monodromy at ![]() $\infty$, then no such result is known; more specifically, the output of his later work on the Langlands correspondence will imply that there exists an open subset
$\infty$, then no such result is known; more specifically, the output of his later work on the Langlands correspondence will imply that there exists an open subset ![]() $V\subset U\times U$ and a smooth projective morphism
$V\subset U\times U$ and a smooth projective morphism ![]() $f\colon S\rightarrow V$ of relative dimension 2 such that
$f\colon S\rightarrow V$ of relative dimension 2 such that ![]() ${\mathbb {L}}\boxtimes {\mathbb {L}}^*|_V$ is a summand of
${\mathbb {L}}\boxtimes {\mathbb {L}}^*|_V$ is a summand of ![]() $R^2f_*\overline {\mathbb {Q}}_{\ell }$. See [Reference KrishnamoorthyKri22, Remark 1.4, Question 9.1] and [Reference Krishnamoorthy and PálKP21, § 1] for related discussion.
$R^2f_*\overline {\mathbb {Q}}_{\ell }$. See [Reference KrishnamoorthyKri22, Remark 1.4, Question 9.1] and [Reference Krishnamoorthy and PálKP21, § 1] for related discussion.
Our argument largely follows [Reference Snowden and TsimermanST18], but we need several new ingredients. To explain this, we quickly reprise their argument in the following remark.
Remark 1.7 (Sketch of [Reference Snowden and TsimermanST18])
For notational simplicity, assume that ![]() $\mathbb {L}$ corresponds to a representation
$\mathbb {L}$ corresponds to a representation
with the property that the mod ![]() $\ell ^3$ residual representation
$\ell ^3$ residual representation ![]() $\pi _1(U_K)\rightarrow \mathrm {GL}_2(\mathbb {Z}/\ell ^3\mathbb {Z})$ is trivial.
$\pi _1(U_K)\rightarrow \mathrm {GL}_2(\mathbb {Z}/\ell ^3\mathbb {Z})$ is trivial.
(1) Using Drinfeld's first work on the Langlands correspondence over finite fields, for all ![]() ${\mathfrak {p}}\gg 0$ they construct families of elliptic curves over
${\mathfrak {p}}\gg 0$ they construct families of elliptic curves over ![]() ${\mathfrak {U}}_{{\mathfrak {p}}}$ with trivial
${\mathfrak {U}}_{{\mathfrak {p}}}$ with trivial ![]() $\ell ^3$ torsion whose monodromy is isomorphic to
$\ell ^3$ torsion whose monodromy is isomorphic to ![]() $\rho |_{{\mathfrak {U}}_{{\mathfrak {p}}}}$. (This involves an implicit isogeny from what is produced by Drinfeld's theorem.) These families, in turn, induce maps
$\rho |_{{\mathfrak {U}}_{{\mathfrak {p}}}}$. (This involves an implicit isogeny from what is produced by Drinfeld's theorem.) These families, in turn, induce maps
where ![]() $\bar {\mathcal {M}}_{1,1}(\ell ^3)$ is the compactified moduli space of elliptic curve with full
$\bar {\mathcal {M}}_{1,1}(\ell ^3)$ is the compactified moduli space of elliptic curve with full ![]() $\ell ^3$ level structure, defined over
$\ell ^3$ level structure, defined over ![]() $\text {Spec}(\mathbb {Z}[1/\ell ])$, and the final target is therefore a hyperbolic curve over
$\text {Spec}(\mathbb {Z}[1/\ell ])$, and the final target is therefore a hyperbolic curve over ![]() $\mathcal {O}_K/{\mathfrak {p}}$.
$\mathcal {O}_K/{\mathfrak {p}}$.
(2) While the map ![]() $\lambda _{{\mathfrak {p}}}$ is not a priori generically separable, they factor it through absolute Frobenius to construct a new map,
$\lambda _{{\mathfrak {p}}}$ is not a priori generically separable, they factor it through absolute Frobenius to construct a new map, ![]() $\mu _{{\mathfrak {p}}}\colon {\mathfrak {X}}_{{\mathfrak {p}}}\rightarrow \bar {\mathcal {M}}_{1,1}(\ell ^3)\otimes \mathcal {O}_K/{\mathfrak {p}}$ which is generically separable. Note that the induced elliptic curve over
$\mu _{{\mathfrak {p}}}\colon {\mathfrak {X}}_{{\mathfrak {p}}}\rightarrow \bar {\mathcal {M}}_{1,1}(\ell ^3)\otimes \mathcal {O}_K/{\mathfrak {p}}$ which is generically separable. Note that the induced elliptic curve over ![]() ${\mathfrak {U}}_{{\mathfrak {p}}}$ also has monodromy isomorphic to
${\mathfrak {U}}_{{\mathfrak {p}}}$ also has monodromy isomorphic to ![]() $\rho |_{{\mathfrak {U}}_{{\mathfrak {p}}}}$. Then Riemann–Hurwitz applies, bounding the degree of the map
$\rho |_{{\mathfrak {U}}_{{\mathfrak {p}}}}$. Then Riemann–Hurwitz applies, bounding the degree of the map ![]() $\mu _{{\mathfrak {p}}}$ by some number
$\mu _{{\mathfrak {p}}}$ by some number ![]() $d$, which is crucially independent of
$d$, which is crucially independent of ![]() ${\mathfrak {p}}$. We may replace
${\mathfrak {p}}$. We may replace ![]() $\lambda _{{\mathfrak {p}}}$ with
$\lambda _{{\mathfrak {p}}}$ with ![]() $\mu _{{\mathfrak {p}}}$.
$\mu _{{\mathfrak {p}}}$.
(3) At this point, consider the moduli space of maps:
of morphisms of curves ![]() $\lambda$ over
$\lambda$ over ![]() ${\mathcal {O}_K[1/N]}$, with degree bounded by
${\mathcal {O}_K[1/N]}$, with degree bounded by ![]() $d$. This moduli space is a scheme of finite type over
$d$. This moduli space is a scheme of finite type over ![]() ${\mathcal {O}_K[1/N]}$ because we have put a bound on the degree.Footnote 2 For each
${\mathcal {O}_K[1/N]}$ because we have put a bound on the degree.Footnote 2 For each ![]() $k$, let
$k$, let ![]() $\mathcal {H}_k$ denote the subset of
$\mathcal {H}_k$ denote the subset of ![]() $\mathcal {H}$ consisting of those maps
$\mathcal {H}$ consisting of those maps ![]() $\lambda$ such that:
$\lambda$ such that:
•
 $\lambda ({\mathfrak {U}})\subset \mathcal {M}_{1,1}(\ell ^3)$; and
$\lambda ({\mathfrak {U}})\subset \mathcal {M}_{1,1}(\ell ^3)$; and• the induced elliptic curve
 $E_U\rightarrow U$ has mod
$E_U\rightarrow U$ has mod  $\ell ^k$ monodromy isomorphic to
$\ell ^k$ monodromy isomorphic to  $\rho \text { mod }\ell ^k$.
$\rho \text { mod }\ell ^k$.
Then Snowden and Tsimerman show that each the ![]() $\mathcal {H}_k$ is a closed subset and, hence, so is
$\mathcal {H}_k$ is a closed subset and, hence, so is ![]() $\mathcal {H}_{\infty }:=\cap \mathcal {H}_k$. The subset
$\mathcal {H}_{\infty }:=\cap \mathcal {H}_k$. The subset ![]() $\mathcal {H}_\infty \subset \mathcal {H}$ will parametrize those maps
$\mathcal {H}_\infty \subset \mathcal {H}$ will parametrize those maps ![]() $\lambda$ such that the monodromy representation is integrally isomorphic to
$\lambda$ such that the monodromy representation is integrally isomorphic to ![]() $\rho$. Equipping
$\rho$. Equipping ![]() $\mathcal {H}_{\infty }\subset \mathcal {H}$ with the reduced induced subscheme structure, they deduce that
$\mathcal {H}_{\infty }\subset \mathcal {H}$ with the reduced induced subscheme structure, they deduce that ![]() $\mathcal {H}_{\infty }$ is therefore a scheme of finite type over
$\mathcal {H}_{\infty }$ is therefore a scheme of finite type over ![]() ${\mathcal {O}_K[1/N]}$. As it has points modulo
${\mathcal {O}_K[1/N]}$. As it has points modulo ![]() ${\mathfrak {p}}$ for infinitely many primes
${\mathfrak {p}}$ for infinitely many primes ![]() ${\mathfrak {p}}$ of
${\mathfrak {p}}$ of ![]() $\mathcal {O}_K$, it follows that it has a point over a finite extension field
$\mathcal {O}_K$, it follows that it has a point over a finite extension field ![]() $K'/K$. Then a Weil restriction argument, together with Faltings’ isogeny theorem, allows one to conclude.
$K'/K$. Then a Weil restriction argument, together with Faltings’ isogeny theorem, allows one to conclude.
We now explain the new ingredients in turn, highlighting the additional difficulties.
Remark 1.8 (Sketch of the proof of Theorem 1.4)
Again for notational simplicity, assume that ![]() $\mathcal {L}$ corresponds to a representation:
$\mathcal {L}$ corresponds to a representation:
(Note that ![]() $\mathbb {Q}_{\ell }$ contains number fields of infinitely large degree.) We further assume that
$\mathbb {Q}_{\ell }$ contains number fields of infinitely large degree.) We further assume that ![]() $\rho$ has the property that the mod
$\rho$ has the property that the mod ![]() $\ell ^3$ residual representation
$\ell ^3$ residual representation ![]() $\pi _1(U_K)\rightarrow \mathrm {GL}_2(\mathbb {Z}/\ell ^3\mathbb {Z})$ is trivial. (This last assumption will play no role, but we include it to see which additional technicalities emerge.)
$\pi _1(U_K)\rightarrow \mathrm {GL}_2(\mathbb {Z}/\ell ^3\mathbb {Z})$ is trivial. (This last assumption will play no role, but we include it to see which additional technicalities emerge.)
(1) Again using Drinfeld's early work on the Langlands correspondence over finite fields, for each ![]() ${\mathfrak {p}}\gg 0$, we may construct an abelian scheme over
${\mathfrak {p}}\gg 0$, we may construct an abelian scheme over ![]() $f_{{\mathfrak {p}}}\colon A_{{\mathfrak {p}}}\rightarrow {\mathfrak {U}}_{{\mathfrak {p}}}$ of dimension
$f_{{\mathfrak {p}}}\colon A_{{\mathfrak {p}}}\rightarrow {\mathfrak {U}}_{{\mathfrak {p}}}$ of dimension ![]() $h:=[E:{\mathbb {Q}}]$, such that
$h:=[E:{\mathbb {Q}}]$, such that ![]() ${\mathcal {L}}|_{{\mathfrak {U}}_{{\mathfrak {p}}}}$ injects as a summand of
${\mathcal {L}}|_{{\mathfrak {U}}_{{\mathfrak {p}}}}$ injects as a summand of ![]() $\mathrm {R}^1f_{{\mathfrak {p}},*}\overline {\mathbb {Q}}_{\ell }$.
$\mathrm {R}^1f_{{\mathfrak {p}},*}\overline {\mathbb {Q}}_{\ell }$.
(a) Here we encounter our first complication: it is not necessarily true that we can choose
 $A_{{\mathfrak {p}}}[\ell ^3]$ to be the split étale cover of
$A_{{\mathfrak {p}}}[\ell ^3]$ to be the split étale cover of  ${\mathfrak {U}}_{{\mathfrak {p}}}$: unlike in the case [Reference Snowden and TsimermanST18],
${\mathfrak {U}}_{{\mathfrak {p}}}$: unlike in the case [Reference Snowden and TsimermanST18],  ${\mathcal {L}}|_{{\mathfrak {U}}_{{\mathfrak {p}}}}$ is not all of
${\mathcal {L}}|_{{\mathfrak {U}}_{{\mathfrak {p}}}}$ is not all of  $\mathrm {R}^1f_{{\mathfrak {p}},*}\overline {\mathbb {Q}}_{\ell }$. However, there exists a finite, connected cover
$\mathrm {R}^1f_{{\mathfrak {p}},*}\overline {\mathbb {Q}}_{\ell }$. However, there exists a finite, connected cover  $\varphi _{{\mathfrak {p}}}\colon ({\mathfrak {X}}_{{\mathfrak {p}}})'\rightarrow {\mathfrak {X}}_{{\mathfrak {p}}}$ (purely in characteristic
$\varphi _{{\mathfrak {p}}}\colon ({\mathfrak {X}}_{{\mathfrak {p}}})'\rightarrow {\mathfrak {X}}_{{\mathfrak {p}}}$ (purely in characteristic  $p$!) of degree
$p$!) of degree  $\leq |\mathrm {GL}_{2h}({\mathbb {Z}}/\ell ^3{\mathbb {Z}})|$ such that:
$\leq |\mathrm {GL}_{2h}({\mathbb {Z}}/\ell ^3{\mathbb {Z}})|$ such that:
• the map
 $\varphi _{{\mathfrak {p}}}$ is finite étale over
$\varphi _{{\mathfrak {p}}}$ is finite étale over  ${\mathfrak {U}}_{{\mathfrak {p}}}$;
${\mathfrak {U}}_{{\mathfrak {p}}}$;• if we set
 $({\mathfrak {U}}_{{\mathfrak {p}}})':=\varphi _{{\mathfrak {p}}}^{-1}({\mathfrak {U}}_{{\mathfrak {p}}})$, the pullback
$({\mathfrak {U}}_{{\mathfrak {p}}})':=\varphi _{{\mathfrak {p}}}^{-1}({\mathfrak {U}}_{{\mathfrak {p}}})$, the pullback  $A'\rightarrow ({\mathfrak {U}}_{{\mathfrak {p}}})'$ has trivial
$A'\rightarrow ({\mathfrak {U}}_{{\mathfrak {p}}})'$ has trivial  $\ell ^3$-torsion;
$\ell ^3$-torsion;• the abelian scheme
 $f'_{{\mathfrak {p}}}\colon A'\rightarrow ({\mathfrak {U}}_{{\mathfrak {p}}})'$ has semistable reduction at
$f'_{{\mathfrak {p}}}\colon A'\rightarrow ({\mathfrak {U}}_{{\mathfrak {p}}})'$ has semistable reduction at  $({\mathfrak {X}}_{{\mathfrak {p}}})'$.
$({\mathfrak {X}}_{{\mathfrak {p}}})'$.
 $\varphi \colon ({\mathfrak {X}}_{{\mathfrak {p}}})'\rightarrow {\mathfrak {X}}_{{\mathfrak {p}}}$ is that the degree is bounded independent of
$\varphi \colon ({\mathfrak {X}}_{{\mathfrak {p}}})'\rightarrow {\mathfrak {X}}_{{\mathfrak {p}}}$ is that the degree is bounded independent of  ${\mathfrak {p}}$. However, we emphasize that, as of yet, there is no preferred
${\mathfrak {p}}$. However, we emphasize that, as of yet, there is no preferred  $X'\rightarrow X$ over
$X'\rightarrow X$ over  $K$ that patches all of these modulo
$K$ that patches all of these modulo  ${\mathfrak {p}}$ covers together. At this point, we demand that
${\mathfrak {p}}$ covers together. At this point, we demand that  $N>|\mathrm {GL}_{2h}({\mathbb {Z}}/\ell ^3{\mathbb {Z}})|$, to ensure that any such
$N>|\mathrm {GL}_{2h}({\mathbb {Z}}/\ell ^3{\mathbb {Z}})|$, to ensure that any such  $\varphi _{\mathfrak {p}}$ is tamely ramified.
$\varphi _{\mathfrak {p}}$ is tamely ramified.(b) We now encounter our next (minor) trouble. A priori, there is no bound on the degree of the polarization of
 $f'_{{\mathfrak {p}}}\colon A'_{{\mathfrak {p}}}\rightarrow ({\mathfrak {U}}_{{\mathfrak {p}}})'$. This has a simple solution: Zarhin's trick, which says that
$f'_{{\mathfrak {p}}}\colon A'_{{\mathfrak {p}}}\rightarrow ({\mathfrak {U}}_{{\mathfrak {p}}})'$. This has a simple solution: Zarhin's trick, which says that  $B'_{{\mathfrak {p}}}:=(A'_{{\mathfrak {p}}}\times (A'_{{\mathfrak {p}}})^t)^4$ has a principal polarization.
$B'_{{\mathfrak {p}}}:=(A'_{{\mathfrak {p}}}\times (A'_{{\mathfrak {p}}})^t)^4$ has a principal polarization.(c) There is a third trouble; unlike in the approach of Snowden and Tsimerman, we have not yet nailed down the integral monodromy, and this is more subtle. There are several ways one could address this. Our solution to this problem will be found in the construction of a simple moduli space,
 $\mathcal {H}_k$: see step (3).
$\mathcal {H}_k$: see step (3).
We therefore get a map:
where ![]() $\mathcal {A}^*_{8h,1,\ell ^3}$ is the Baily–Borel compactification of the fine moduli scheme
$\mathcal {A}^*_{8h,1,\ell ^3}$ is the Baily–Borel compactification of the fine moduli scheme ![]() $\mathcal {A}_{8h,1,\ell ^3}$ parametrizing principally polarized abelian schemes of dimension
$\mathcal {A}_{8h,1,\ell ^3}$ parametrizing principally polarized abelian schemes of dimension ![]() $8h$ and trivial level
$8h$ and trivial level ![]() $\ell ^3$ structure. This
$\ell ^3$ structure. This ![]() $\lambda '_{{\mathfrak {p}}}$ has the following property: the pullback of the universal rank
$\lambda '_{{\mathfrak {p}}}$ has the following property: the pullback of the universal rank ![]() $16h$ lisse
$16h$ lisse ![]() $\ell$-adic sheaf on
$\ell$-adic sheaf on ![]() $\mathcal {A}_{8h,1,\ell ^3}$ to
$\mathcal {A}_{8h,1,\ell ^3}$ to ![]() ${\mathfrak {U}}_{{\mathfrak {p}}}$ has
${\mathfrak {U}}_{{\mathfrak {p}}}$ has ![]() $\rho$ as a rational summand.
$\rho$ as a rational summand.
(2) Our next goal is to somehow numerically bound ![]() $\lambda '_{{\mathfrak {p}}}$. Recall that [Reference Snowden and TsimermanST18] do this by a combination of Riemann–Hurwitz and factoring through some power of absolute Frobenius. In our setting, this step is more tricky, and we chose to use an Arakelov-style inequality. More precisely, if
$\lambda '_{{\mathfrak {p}}}$. Recall that [Reference Snowden and TsimermanST18] do this by a combination of Riemann–Hurwitz and factoring through some power of absolute Frobenius. In our setting, this step is more tricky, and we chose to use an Arakelov-style inequality. More precisely, if ![]() $f_{\mathfrak {p}}: \bar {B'}_{{\mathfrak {p}}}\rightarrow ({\mathfrak {X}}_{{\mathfrak {p}}})'$ is the Néron model of
$f_{\mathfrak {p}}: \bar {B'}_{{\mathfrak {p}}}\rightarrow ({\mathfrak {X}}_{{\mathfrak {p}}})'$ is the Néron model of ![]() $B'_{{\mathfrak {p}}}\rightarrow {\mathfrak {U}}_{{\mathfrak {p}}}',$ then we will bound the degree of the Hodge vector bundle
$B'_{{\mathfrak {p}}}\rightarrow {\mathfrak {U}}_{{\mathfrak {p}}}',$ then we will bound the degree of the Hodge vector bundle ![]() $E^{1,0}_{({\mathfrak {X}}_{{\mathfrak {p}}})'}:=R^0{f_{\mathfrak {p}}}_*\Omega ^1_{\bar {B'}_{{\mathfrak {p}}}/ ({\mathfrak {X}}_{\mathfrak {p}})' }(\log \Delta )$, at least for many infinitely many
$E^{1,0}_{({\mathfrak {X}}_{{\mathfrak {p}}})'}:=R^0{f_{\mathfrak {p}}}_*\Omega ^1_{\bar {B'}_{{\mathfrak {p}}}/ ({\mathfrak {X}}_{\mathfrak {p}})' }(\log \Delta )$, at least for many infinitely many ![]() ${\mathfrak {p}}$. Set
${\mathfrak {p}}$. Set ![]() $E^{0,1}_{({\mathfrak {X}}_{{\mathfrak {p}}})'}:=R^1{f_p}_*\mathcal {O}_{ \bar {B'}_{{\mathfrak {p}}} }$. Then to bound the degree of
$E^{0,1}_{({\mathfrak {X}}_{{\mathfrak {p}}})'}:=R^1{f_p}_*\mathcal {O}_{ \bar {B'}_{{\mathfrak {p}}} }$. Then to bound the degree of ![]() $E^{1,0}_{({\mathfrak {X}}_{{\mathfrak {p}}})'}$, we will need to know that the logarithmic Kodaira–Spencer map constructed by Faltings and Chai,
$E^{1,0}_{({\mathfrak {X}}_{{\mathfrak {p}}})'}$, we will need to know that the logarithmic Kodaira–Spencer map constructed by Faltings and Chai,
is not only non-zero but is moreover an isomorphism at the generic point.Footnote 3 In more detail: for any ![]() ${\mathfrak {p}}\gg 0$ such that the underlying prime number
${\mathfrak {p}}\gg 0$ such that the underlying prime number ![]() $p$ splits completely in
$p$ splits completely in ![]() $E$, the field generated by Frobenius traces, the induced
$E$, the field generated by Frobenius traces, the induced ![]() $p$-divisible group on
$p$-divisible group on ![]() $({\mathfrak {U}}_{{\mathfrak {p}}})'$ splits as the direct sum of several copies of
$({\mathfrak {U}}_{{\mathfrak {p}}})'$ splits as the direct sum of several copies of ![]() $h$ (mutually non-isogenous) height
$h$ (mutually non-isogenous) height ![]() $2$, dimension
$2$, dimension ![]() $1$
$1$ ![]() $p$-divisible groups
$p$-divisible groups ![]() $G'_i$ and their duals
$G'_i$ and their duals ![]() $(G'_i)^t$. We prove, using monodromy considerations, that they are generically ordinary and have supersingular points. Applying a Frobenius untwisting lemma from the PhD thesis of Jie Xia [Reference XiaXia13], we conclude that we may ‘Frobenius untwist’ each of them until they are all generically versally deformed.Footnote 4 (In Appendix A, we provide a proof of Xia's Frobenius untwisting lemma in our context, and also give a second argument and perspective of the termination of Frobenius untwisting stability techniques.) Once again using Zarhin's trick, we will obtain an isogenous, principally polarized abelian scheme over
$(G'_i)^t$. We prove, using monodromy considerations, that they are generically ordinary and have supersingular points. Applying a Frobenius untwisting lemma from the PhD thesis of Jie Xia [Reference XiaXia13], we conclude that we may ‘Frobenius untwist’ each of them until they are all generically versally deformed.Footnote 4 (In Appendix A, we provide a proof of Xia's Frobenius untwisting lemma in our context, and also give a second argument and perspective of the termination of Frobenius untwisting stability techniques.) Once again using Zarhin's trick, we will obtain an isogenous, principally polarized abelian scheme over ![]() ${\mathfrak {U}}_{{\mathfrak {p}}}'$, which we relabel
${\mathfrak {U}}_{{\mathfrak {p}}}'$, which we relabel ![]() $B'_{{\mathfrak {p}}}$, with the Néron model
$B'_{{\mathfrak {p}}}$, with the Néron model
and such that the logarithmic Kodaira–Spencer map is a generically injective map of coherent sheaves on ![]() $({\mathfrak {X}}_{{\mathfrak {p}}})'$. By taking determinants, we deduce an Arakelov-style inequality, thereby bounding the degree of the induced Hodge line bundle on
$({\mathfrak {X}}_{{\mathfrak {p}}})'$. By taking determinants, we deduce an Arakelov-style inequality, thereby bounding the degree of the induced Hodge line bundle on ![]() $({\mathfrak {X}}_{{\mathfrak {p}}})'$ by some integer
$({\mathfrak {X}}_{{\mathfrak {p}}})'$ by some integer ![]() $d$, which is crucially independent of
$d$, which is crucially independent of ![]() ${\mathfrak {p}}$. The output of this is Lemma 2.7.
${\mathfrak {p}}$. The output of this is Lemma 2.7.
(3) To mimic the third step, we first construct some finite-type moduli spaces of ![]() ${\mathcal {O}_K[1/N]}$, and then we use our argument as above to show it has points modulo
${\mathcal {O}_K[1/N]}$, and then we use our argument as above to show it has points modulo ![]() ${\mathfrak {p}}$ for infinitely many
${\mathfrak {p}}$ for infinitely many ![]() ${\mathfrak {p}}$. This is, in greater detail, as follows.
${\mathfrak {p}}$. This is, in greater detail, as follows.
(a) Fix
 $d>1$ and set
$d>1$ and set  $\mathcal {H}$ to be the moduli of triples
$\mathcal {H}$ to be the moduli of triples  $({\mathfrak {X}}',\varphi,\lambda )$:
where:
$({\mathfrak {X}}',\varphi,\lambda )$:
where:
•
 ${\mathfrak {X}}'/{\mathcal {O}_K[1/N]}$ is a smooth, proper, geometrically connected curve;
${\mathfrak {X}}'/{\mathcal {O}_K[1/N]}$ is a smooth, proper, geometrically connected curve;•
 $\varphi$ is finite, of degree at most
$\varphi$ is finite, of degree at most  $\leq |\mathrm {GL}_{16h}({\mathbb {Z}}/\ell ^3{\mathbb {Z}})|$, and étale over
$\leq |\mathrm {GL}_{16h}({\mathbb {Z}}/\ell ^3{\mathbb {Z}})|$, and étale over  ${\mathfrak {U}}$;
${\mathfrak {U}}$;• there exists some point
 $\infty '\in {\mathfrak {X}}'$ that is sent to a
$\infty '\in {\mathfrak {X}}'$ that is sent to a  $0$-dimensional cusp in
$0$-dimensional cusp in  $\mathscr {A}^*_{8h,1,\ell ^3}$; and
$\mathscr {A}^*_{8h,1,\ell ^3}$; and• the degree of the pulled-back Hodge line bundle on
 ${\mathfrak {X}}'_K$ is
${\mathfrak {X}}'_K$ is  $\leq d$.
$\leq d$.
 $\mathcal {H}$ will be a Deligne–Mumford stack, of finite type over
$\mathcal {H}$ will be a Deligne–Mumford stack, of finite type over  ${\mathcal {O}_K[1/N]}$. (The stackiness comes from the intervening Hurwitz space.) We further show that the generic fiber of
${\mathcal {O}_K[1/N]}$. (The stackiness comes from the intervening Hurwitz space.) We further show that the generic fiber of  $\mathcal {H}$ has dimension
$\mathcal {H}$ has dimension  $0$ (and is, in fact, reduced); while this is an immediate corollary of the PhD thesis of Ben Moonen [Reference MoonenMoo98], we argue following the work of Saito. This implies that, after potentially further increasing
$0$ (and is, in fact, reduced); while this is an immediate corollary of the PhD thesis of Ben Moonen [Reference MoonenMoo98], we argue following the work of Saito. This implies that, after potentially further increasing  $N$, the stack
$N$, the stack  $\mathcal {H}/{\mathcal {O}_K[1/N]}$ has relative dimension
$\mathcal {H}/{\mathcal {O}_K[1/N]}$ has relative dimension  $0$.Footnote 5
$0$.Footnote 5(b) Recall that
 $\mathcal {L}$ is a lisse
$\mathcal {L}$ is a lisse  $\mathbb {Z}_{\ell }$-sheaf on
$\mathbb {Z}_{\ell }$-sheaf on  ${\mathfrak {U}}$, whose generic fiber is an
${\mathfrak {U}}$, whose generic fiber is an  $\mathbb {Z}_{\ell }$-lattice inside of
$\mathbb {Z}_{\ell }$-lattice inside of  ${\mathbb {L}}$. For
${\mathbb {L}}$. For  $k\geq 1$, set
$k\geq 1$, set  $\mathcal {H}_k$ to be the subspace of
$\mathcal {H}_k$ to be the subspace of  $\mathcal {H}$ given by those
$\mathcal {H}$ given by those  $({\mathfrak {X}}',\varphi,\lambda )$ (with induced abelian scheme
$({\mathfrak {X}}',\varphi,\lambda )$ (with induced abelian scheme  $f\colon B'\rightarrow {\mathfrak {X}}'$) such that there exists a map
of torsion locally constant étale sheaves with the following condition: the reduction modulo
$f\colon B'\rightarrow {\mathfrak {X}}'$) such that there exists a map
of torsion locally constant étale sheaves with the following condition: the reduction modulo \[ \psi\colon \varphi^*(\mathcal{L})/\ell^k\rightarrow R^1f_* {\mathbb{Z}}_{\ell}/\ell^k \]
\[ \psi\colon \varphi^*(\mathcal{L})/\ell^k\rightarrow R^1f_* {\mathbb{Z}}_{\ell}/\ell^k \]
 $\ell$ of
$\ell$ of  $\psi$ is non-zero. (This condition is crucial in our approach.)Footnote 6 Then
$\psi$ is non-zero. (This condition is crucial in our approach.)Footnote 6 Then  $\mathcal {H}_k\subset \mathcal {H}$ will be a closed substack, which we may equip with the reduced induced structure. Similarly, set
$\mathcal {H}_k\subset \mathcal {H}$ will be a closed substack, which we may equip with the reduced induced structure. Similarly, set  $\mathcal {H}_{\infty }$ to be
$\mathcal {H}_{\infty }$ to be  $\cap \mathcal {H}_k$, again with the reduced induced stack structure. Note that
$\cap \mathcal {H}_k$, again with the reduced induced stack structure. Note that  $\mathcal {H}_{\infty }$ is then a finite-type Deligne–Mumford stack over
$\mathcal {H}_{\infty }$ is then a finite-type Deligne–Mumford stack over  $\text {Spec}({\mathcal {O}_K[1/N]})$ for some
$\text {Spec}({\mathcal {O}_K[1/N]})$ for some  $N$.
$N$.
Unlike in the Snowden–Tsimerman approach, the relationship of the moduli space
 $\mathcal {H}_{\infty }$ to Drinfeld's theorem is not immediately apparent. However, in both approaches, the moduli spaces involve extra maps of
$\mathcal {H}_{\infty }$ to Drinfeld's theorem is not immediately apparent. However, in both approaches, the moduli spaces involve extra maps of  $\ell ^k$-torsion sheaves rather than lisse
$\ell ^k$-torsion sheaves rather than lisse  $\mathbb {Z}_{\ell }$-sheaves.
$\mathbb {Z}_{\ell }$-sheaves.(c) By the careful choice of
 $\mathcal {H}_k$ and a crucial diagonalization argument on
$\mathcal {H}_k$ and a crucial diagonalization argument on  $\mathcal {H}_{\infty }$ (contained in Lemma 3.6), it will follow from the earlier steps that there exists an infinite set of primes
$\mathcal {H}_{\infty }$ (contained in Lemma 3.6), it will follow from the earlier steps that there exists an infinite set of primes  ${\mathfrak {p}}$ such that
${\mathfrak {p}}$ such that  $\mathcal {H}_{\infty }$ has points modulo
$\mathcal {H}_{\infty }$ has points modulo  ${\mathfrak {p}}$. (Unlike the approach of Snowden and Tsimerman, this does not require one to take an
${\mathfrak {p}}$. (Unlike the approach of Snowden and Tsimerman, this does not require one to take an  $\ell$-primary isogeny.) By the Nullstellensatz, one deduces that
$\ell$-primary isogeny.) By the Nullstellensatz, one deduces that  $\mathcal {H}_{\infty }$ has characteristic
$\mathcal {H}_{\infty }$ has characteristic  $0$ points. A Weil restriction argument then yields the result.
$0$ points. A Weil restriction argument then yields the result.
Remark 1.9 Katz has shown that rigid local systems on the punctured projective line are motivic, and Corlette and Simpson have shown that all rigid rank 2 local systems are motivic. Our main theorem provides a new arithmetic approach to both Katz's theorem in rank 2 and also the Corlette–Simpson theorem, subject to an additional assumption analogous to condition ![]() $(4)$. Here is an outline of the proof. We emphasize that these approaches will critically rely on a quasi-projective version of a deep theorem on projective varieties of Esnault and Groechenig [Reference Esnault and GroechenigEG20]; this result was announced very recently [Reference Esnault and GroechenigEG23].
$(4)$. Here is an outline of the proof. We emphasize that these approaches will critically rely on a quasi-projective version of a deep theorem on projective varieties of Esnault and Groechenig [Reference Esnault and GroechenigEG20]; this result was announced very recently [Reference Esnault and GroechenigEG23].
First we assume that ![]() $U$ is a curve. Let
$U$ is a curve. Let ![]() ${\mathbb {L}}$ be a cohomologically rigid local system of rank
${\mathbb {L}}$ be a cohomologically rigid local system of rank ![]() $2$ on
$2$ on ![]() $U^{an}_{\mathbb {C}}$ with coefficients in
$U^{an}_{\mathbb {C}}$ with coefficients in ![]() $\overline {\mathbb {Q}}_{\ell }$, trivial determinant and infinite monodromy around
$\overline {\mathbb {Q}}_{\ell }$, trivial determinant and infinite monodromy around ![]() $\infty$. Suppose that the local system
$\infty$. Suppose that the local system ![]() ${\mathbb {L}}$ spreads out to an étale local system
${\mathbb {L}}$ spreads out to an étale local system ![]() $\mathcal {L}$ with cyclotomic determinant over a finitely generated spreading out
$\mathcal {L}$ with cyclotomic determinant over a finitely generated spreading out ![]() $\mathfrak {U}/S$ such that the stable Frobenius trace fields are bounded, i.e. there exists a number field
$\mathfrak {U}/S$ such that the stable Frobenius trace fields are bounded, i.e. there exists a number field ![]() $E$ such that for all closed points
$E$ such that for all closed points ![]() $s$, there exists a finite extension
$s$, there exists a finite extension ![]() $s'/s$ such that the Frobenius trace field of
$s'/s$ such that the Frobenius trace field of ![]() $\mathcal {L}|_{\mathfrak {U}_{s'}}$ is contained in
$\mathcal {L}|_{\mathfrak {U}_{s'}}$ is contained in ![]() $E$. Then, our argument applies verbatim to prove that
$E$. Then, our argument applies verbatim to prove that ![]() ${\mathbb {L}}$ over
${\mathbb {L}}$ over ![]() $U_{\mathbb {C}}$ comes from a family of abelian varieties; we get mod
$U_{\mathbb {C}}$ comes from a family of abelian varieties; we get mod ![]() $p$ points for infinitely many
$p$ points for infinitely many ![]() $p\gg 0$, and the relevant moduli space is of finite type and, in fact, generically
$p\gg 0$, and the relevant moduli space is of finite type and, in fact, generically ![]() $0$-dimensional, so by specialization of the prime-to-
$0$-dimensional, so by specialization of the prime-to-![]() $p$ fundamental group we may conclude.
$p$ fundamental group we may conclude.
In fact, recent work [Reference Krishnamoorthy and LamKL23] of the first-named author and Lam shows the following. If ![]() $X/\mathbb {C}$ is a projective variety, and if
$X/\mathbb {C}$ is a projective variety, and if ![]() ${\mathbb {L}}$ is a cohomologically rigid
${\mathbb {L}}$ is a cohomologically rigid ![]() $\overline {\mathbb {Q}}_{\ell }$-local system with trivial determinant on
$\overline {\mathbb {Q}}_{\ell }$-local system with trivial determinant on ![]() $X^{an}$, then there exists a spreading out
$X^{an}$, then there exists a spreading out ![]() $\mathfrak {X}/S$ and a number field
$\mathfrak {X}/S$ and a number field ![]() $E\subset \overline {\mathbb {Q}}_{\ell }$ such that
$E\subset \overline {\mathbb {Q}}_{\ell }$ such that ![]() ${\mathbb {L}}$ spreads out to an étale local system
${\mathbb {L}}$ spreads out to an étale local system ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $\mathfrak {X}$ with cyclotomic determinant such that the stable Frobenius trace field is contained inside of
$\mathfrak {X}$ with cyclotomic determinant such that the stable Frobenius trace field is contained inside of ![]() $E$. In the quasi-projective case, which is what is needed here, the arguments of [Reference Krishnamoorthy and LamKL23] work mutatis mutandis, substituting in [Reference Esnault and GroechenigEG23] for [Reference Esnault and GroechenigEG20]. Indeed, in [Reference Krishnamoorthy and LamKL23], the key
$E$. In the quasi-projective case, which is what is needed here, the arguments of [Reference Krishnamoorthy and LamKL23] work mutatis mutandis, substituting in [Reference Esnault and GroechenigEG23] for [Reference Esnault and GroechenigEG20]. Indeed, in [Reference Krishnamoorthy and LamKL23], the key ![]() $p$-adic fact we need is that rigid stable flat connections give rise to
$p$-adic fact we need is that rigid stable flat connections give rise to ![]() $F^f$-isocrystals on the relevant
$F^f$-isocrystals on the relevant ![]() $p$-adic completions.
$p$-adic completions.
In general, when ![]() $U$ is higher dimensional (i.e.
$U$ is higher dimensional (i.e. ![]() $U=X\setminus D$, where
$U=X\setminus D$, where ![]() $X$ is a smooth projective variety and
$X$ is a smooth projective variety and ![]() $D$ is a simple normal crossings divisor), it is very plausible that one may similarly deduce the analog of the Corlette–Simpson theorem here (again, subject to the restriction that the local system is cohomologically rigid and that the local monodromy around one of the boundary divisors is infinite). Here is a sketch of the argument. The main results of [Reference Esnault and GroechenigEG23] in fact output rank 2 filtered logarithmic
$D$ is a simple normal crossings divisor), it is very plausible that one may similarly deduce the analog of the Corlette–Simpson theorem here (again, subject to the restriction that the local system is cohomologically rigid and that the local monodromy around one of the boundary divisors is infinite). Here is a sketch of the argument. The main results of [Reference Esnault and GroechenigEG23] in fact output rank 2 filtered logarithmic ![]() $F$-crystals; as above, porting these objects into [Reference Krishnamoorthy and LamKL23] as above, one can deduce that cohomologically rigid rank 2 local systems will have spreading-outs whose stable Frobenius trace field is bounded. A complete set of companions to the logarithmic
$F$-crystals; as above, porting these objects into [Reference Krishnamoorthy and LamKL23] as above, one can deduce that cohomologically rigid rank 2 local systems will have spreading-outs whose stable Frobenius trace field is bounded. A complete set of companions to the logarithmic ![]() $F$-isocrystals so constructed will likely exist, as in the projective case this is shown in [Reference Esnault and GroechenigEG20]. From these
$F$-isocrystals so constructed will likely exist, as in the projective case this is shown in [Reference Esnault and GroechenigEG20]. From these ![]() $F$-isocrystals, [Reference Krishnamoorthy and PálKP22] will provide abelian schemes on open subsets of the mod
$F$-isocrystals, [Reference Krishnamoorthy and PálKP22] will provide abelian schemes on open subsets of the mod ![]() $p$ fibers of bounded dimensionFootnote 7 and [Reference Krishnamoorthy and PálKP21, Corollary 6.12] shows that, after possibly replacing with an isogenous abelian scheme, the abelian schemes extend to the whole mod
$p$ fibers of bounded dimensionFootnote 7 and [Reference Krishnamoorthy and PálKP21, Corollary 6.12] shows that, after possibly replacing with an isogenous abelian scheme, the abelian schemes extend to the whole mod ![]() $p$ fiber of
$p$ fiber of ![]() $\mathfrak {U}$. We can bound the degree of the Hodge line bundle for infinitely many
$\mathfrak {U}$. We can bound the degree of the Hodge line bundle for infinitely many ![]() $p$ by Frobenius untwisting, exactly as is done here. Finally, the appropriate Hom scheme will again be
$p$ by Frobenius untwisting, exactly as is done here. Finally, the appropriate Hom scheme will again be ![]() $0$-dimensional, so by using specialization of the prime-to-
$0$-dimensional, so by using specialization of the prime-to-![]() $p$ fundamental group one may again conclude.
$p$ fundamental group one may again conclude.
2. Drinfeld's work on the Langlands correspondence for  $\mathrm {GL}_2$ and some corollaries
$\mathrm {GL}_2$ and some corollaries
A key ingredient in the proof of Theorem 1.4 is the following Theorem 2.2, which is a byproduct of Drinfeld's first work on the Langlands correspondence for ![]() $\mathrm {GL}_2$. We first record a setup.
$\mathrm {GL}_2$. We first record a setup.
Setup 2.1 Let ![]() $p$ be a prime number and let
$p$ be a prime number and let ![]() $q=p^a$. Let
$q=p^a$. Let ![]() $C/\mathbb {F}_q$ be a smooth, affine, geometrically irreducible curve with smooth compactification
$C/\mathbb {F}_q$ be a smooth, affine, geometrically irreducible curve with smooth compactification ![]() $\bar {C}$. Let
$\bar {C}$. Let ![]() $Z:=\bar {C}\setminus C$ be the reduced complementary divisor.
$Z:=\bar {C}\setminus C$ be the reduced complementary divisor.
Theorem 2.2 (Drinfeld)
Let the notation be as in Setup 2.1 and let ![]() ${\mathbb {L}}$ be a rank 2 irreducible
${\mathbb {L}}$ be a rank 2 irreducible ![]() $\overline {\mathbb {Q}}_{\ell }$ sheaf on
$\overline {\mathbb {Q}}_{\ell }$ sheaf on ![]() $C$ with determinant
$C$ with determinant ![]() $\overline {\mathbb {Q}}_{\ell }(1)$. Suppose
$\overline {\mathbb {Q}}_{\ell }(1)$. Suppose ![]() ${\mathbb {L}}$ has infinite local monodromy around some point at
${\mathbb {L}}$ has infinite local monodromy around some point at ![]() $\infty \in Z$. Then
$\infty \in Z$. Then ![]() ${\mathbb {L}}$ comes from a family of abelian varieties in the following sense: let
${\mathbb {L}}$ comes from a family of abelian varieties in the following sense: let ![]() $E$ be the field generated by the Frobenius traces of
$E$ be the field generated by the Frobenius traces of ![]() ${\mathbb {L}}$ and suppose
${\mathbb {L}}$ and suppose ![]() $[E:\mathbb {Q}]=h$. Then there exists an abelian scheme
$[E:\mathbb {Q}]=h$. Then there exists an abelian scheme
of dimension ![]() $h$ and an isomorphism
$h$ and an isomorphism ![]() $E\cong \textrm {End}_{C}(A)\otimes \mathbb {Q}$, realizing
$E\cong \textrm {End}_{C}(A)\otimes \mathbb {Q}$, realizing ![]() $A_C$ as a
$A_C$ as a ![]() $\mathrm {SL}_2$-type abelian scheme, such that
$\mathrm {SL}_2$-type abelian scheme, such that ![]() ${\mathbb {L}}$ occurs as a summand of
${\mathbb {L}}$ occurs as a summand of ![]() $R^1(\pi _C)_*\overline {\mathbb {Q}}_{\ell }$. Moreover,
$R^1(\pi _C)_*\overline {\mathbb {Q}}_{\ell }$. Moreover, ![]() $A_{C}\rightarrow C$ is totally degenerate around
$A_{C}\rightarrow C$ is totally degenerate around ![]() $\infty$.
$\infty$.
See [Reference Snowden and TsimermanST18, Proof of Proposition 19, Remark 20] for how to recover this result from Drinfeld's work. This amounts to combining [Reference DrinfeldDri83, Main Theorem, Remark 5] with [Reference Drinfel'dDri77, Theorem 1].
We make some observations about the ![]() $p$-adic properties of the resulting abelian schemes. In particular, our goal is to show that, in the context of Theorem 2.2, we can modify
$p$-adic properties of the resulting abelian schemes. In particular, our goal is to show that, in the context of Theorem 2.2, we can modify ![]() ${A_C\rightarrow C}$ with products, duals, and isogenies such that the resulting abelian scheme
${A_C\rightarrow C}$ with products, duals, and isogenies such that the resulting abelian scheme ![]() $B_C\rightarrow C$ that has especially nice (
$B_C\rightarrow C$ that has especially nice (![]() $p$-adic) properties; these will, in turn, allow us to prove an Arakelov-style inequality. First, we will give the following non-standard definition, which is adapted for our purpose.
$p$-adic) properties; these will, in turn, allow us to prove an Arakelov-style inequality. First, we will give the following non-standard definition, which is adapted for our purpose.
Definition 2.3 Maintain notation as in Setup 2.1. Let ![]() $G_C$ be a
$G_C$ be a ![]() $p$-divisible group on
$p$-divisible group on ![]() $C$. We say
$C$. We say ![]() $G_C$ has strong strict semistable reduction along
$G_C$ has strong strict semistable reduction along ![]() $Z$ if:
$Z$ if:
•
 $G_C$ has semistable reduction along
$G_C$ has semistable reduction along  $Z$ (see [Reference TrihanTri08, Definition 4.2]), which is based on semistable reduction in the sense of de Jong [Reference de JongdJ98, Definition 2.2]; and
$Z$ (see [Reference TrihanTri08, Definition 4.2]), which is based on semistable reduction in the sense of de Jong [Reference de JongdJ98, Definition 2.2]; and• if for every point
 $\infty \in \bar {C}\backslash C$ with local parameter
$\infty \in \bar {C}\backslash C$ with local parameter  $z_{\infty }$ the restricted
$z_{\infty }$ the restricted  $p$-divisible group
over
$p$-divisible group
over \[ G_C|_{\text{Spec}(\mathbb{F}_q((z_{\infty})))} \]
\[ G_C|_{\text{Spec}(\mathbb{F}_q((z_{\infty})))} \]
 $\text {Spec}(\mathbb {F}_q((z_{\infty })))$ does not extend to a
$\text {Spec}(\mathbb {F}_q((z_{\infty })))$ does not extend to a  $p$-divisible group over
$p$-divisible group over  $\text {Spec}(\mathbb {F}_q[[z_{\infty }]]).$
$\text {Spec}(\mathbb {F}_q[[z_{\infty }]]).$
Definition 2.3 is useful as it concisely expresses the condition that ![]() $G_C$ have semistable reduction and, moreover, that it does not extend as a
$G_C$ have semistable reduction and, moreover, that it does not extend as a ![]() $p$-divisible group across any of the cusps.
$p$-divisible group across any of the cusps.
The next proposition will be critical for bounding degrees of maps to moduli spaces. In Appendix A, we explain a second proof/perspective of the second part, which is based on a destabilizing iteration argument due to Langer.
Proposition 2.4 Maintain notation as in Setup 2.1. Let ![]() $G_C$ be a height
$G_C$ be a height ![]() $2$, dimension
$2$, dimension ![]() $1$
$1$ ![]() $p$-divisible group on
$p$-divisible group on ![]() $C$ with strong strict semistable reduction along
$C$ with strong strict semistable reduction along ![]() $Z$. Suppose further that
$Z$. Suppose further that ![]() $\mathbb {D}(G_C)\otimes \overline {\mathbb {Q}}_p$ is an irreducible object of
$\mathbb {D}(G_C)\otimes \overline {\mathbb {Q}}_p$ is an irreducible object of ![]() $\mathbf {F\text{-}Isoc}^{{\dagger} }(C)_{\overline {\mathbb {Q}}_p}$. Then:
$\mathbf {F\text{-}Isoc}^{{\dagger} }(C)_{\overline {\mathbb {Q}}_p}$. Then:
(1)
 $G_C$ is generically ordinary with a non-empty supersingular locus; and
$G_C$ is generically ordinary with a non-empty supersingular locus; and(2) there exists an isogenous
 $p$-divisible group
$p$-divisible group  $H_C\rightarrow G_C$ that is generically versally deformed (in the sense of [Reference KrishnamoorthyKri22, Defintions 8.1, 8.2]).Footnote 8
$H_C\rightarrow G_C$ that is generically versally deformed (in the sense of [Reference KrishnamoorthyKri22, Defintions 8.1, 8.2]).Footnote 8
Before we begin the proof, we comment on the overconvergence assumption. If ![]() $H_C\rightarrow C$ is a
$H_C\rightarrow C$ is a ![]() $p$-divisible group, then
$p$-divisible group, then ![]() $F$-isocrystal
$F$-isocrystal ![]() $\mathbb {D}(H_C)$ is automatically a convergent
$\mathbb {D}(H_C)$ is automatically a convergent ![]() $F$-isocrystal. In our setting, the fact that we demand
$F$-isocrystal. In our setting, the fact that we demand ![]() $G_C\rightarrow C$ to be semistable around
$G_C\rightarrow C$ to be semistable around ![]() $Z$ implies that
$Z$ implies that ![]() $\mathbb {D}(G_C)$ is, in fact, overconvergent. Part of the hypothesis of Proposition 2.4 is then that
$\mathbb {D}(G_C)$ is, in fact, overconvergent. Part of the hypothesis of Proposition 2.4 is then that ![]() $\mathbb {D}(G_C)\otimes \mathbb {Q}_p$ is absolutely irreducible in
$\mathbb {D}(G_C)\otimes \mathbb {Q}_p$ is absolutely irreducible in ![]() $\textbf {F-Isoc}^{{\dagger} }(C)$.
$\textbf {F-Isoc}^{{\dagger} }(C)$.
First proof of Proposition 2.4 As ![]() $G_C$ has height
$G_C$ has height ![]() $2$ and dimension
$2$ and dimension ![]() $1$, there are only two possible Newton polygons, which correspond to the
$1$, there are only two possible Newton polygons, which correspond to the ![]() $p$-divisible group being ordinary or supersingular, respectively. If
$p$-divisible group being ordinary or supersingular, respectively. If ![]() $G_C$ were not generically ordinary, it would be everywhere supersingular. However, supersingular
$G_C$ were not generically ordinary, it would be everywhere supersingular. However, supersingular ![]() $p$-divisible groups cannot be strictly semistable: as there is no multiplicative part, the filtration in [Reference de JongdJ98, Definition 2.2], would have to be trivial, which would imply that
$p$-divisible groups cannot be strictly semistable: as there is no multiplicative part, the filtration in [Reference de JongdJ98, Definition 2.2], would have to be trivial, which would imply that ![]() $G_C$ extends to a
$G_C$ extends to a ![]() $p$-divisible group over
$p$-divisible group over ![]() $\bar {C}$. This shows
$\bar {C}$. This shows ![]() $G_C$ is generically ordinary.
$G_C$ is generically ordinary.
Suppose that ![]() $G_C$ had no supersingular points: then
$G_C$ had no supersingular points: then ![]() $G_C$ is everywhere ordinary. Let
$G_C$ is everywhere ordinary. Let ![]() $H_C$ be the multiplicative sub-
$H_C$ be the multiplicative sub-![]() $p$-divisible group of
$p$-divisible group of ![]() $G_C$, i.e. the height
$G_C$, i.e. the height ![]() $1$, dimension
$1$, dimension ![]() $1$
$1$ ![]() $p$-divisible group with Newton slope
$p$-divisible group with Newton slope ![]() $1$ everywhere. Let
$1$ everywhere. Let ![]() $\infty \in Z$, with formal parameter
$\infty \in Z$, with formal parameter ![]() $z_{\infty }$. Then the
$z_{\infty }$. Then the ![]() $p$-divisible group
$p$-divisible group ![]() $G_C|_{\text {Spec}(\mathbb {F}_q((z_{\infty })))}$ has semistable reduction in the sense of [Reference de JongdJ98, Definition 2.2] and does not extend to a
$G_C|_{\text {Spec}(\mathbb {F}_q((z_{\infty })))}$ has semistable reduction in the sense of [Reference de JongdJ98, Definition 2.2] and does not extend to a ![]() $p$-divisible group over
$p$-divisible group over ![]() $\text {Spec}(\mathbb {F}_q[[z_{\infty }]])$. Then, for the definition of semistability to be satisfied, the only possible filtration is
$\text {Spec}(\mathbb {F}_q[[z_{\infty }]])$. Then, for the definition of semistability to be satisfied, the only possible filtration is
(Here, the meaning of ![]() $G^{\mu }_{\text {Spec}(\mathbb {F}_q((z_{\infty })))}$ and
$G^{\mu }_{\text {Spec}(\mathbb {F}_q((z_{\infty })))}$ and ![]() $G^f_{\text {Spec}(\mathbb {F}_q((z_{\infty })))}$ is given as in [Reference de JongdJ98, Definition 2.2].)
$G^f_{\text {Spec}(\mathbb {F}_q((z_{\infty })))}$ is given as in [Reference de JongdJ98, Definition 2.2].)
However, by the definition of semistability, ![]() $H_C|_{\text {Spec}(\mathbb {F}_q((z_{\infty })))}$ therefore extends to a
$H_C|_{\text {Spec}(\mathbb {F}_q((z_{\infty })))}$ therefore extends to a ![]() $p$-divisible group over
$p$-divisible group over ![]() $\text {Spec}(\mathbb {F}_q[[z_{\infty }]])$. Ranging over all points
$\text {Spec}(\mathbb {F}_q[[z_{\infty }]])$. Ranging over all points ![]() $\infty \in Z$, we see that
$\infty \in Z$, we see that ![]() $\mathbb {D}(H_C)\otimes \mathbb {Q}_p \in \textbf {F-Isoc}(C)$ in fact extends to an
$\mathbb {D}(H_C)\otimes \mathbb {Q}_p \in \textbf {F-Isoc}(C)$ in fact extends to an ![]() $F$-isocrystal on
$F$-isocrystal on ![]() $\textbf {F-Isoc}(\bar {C})$: therefore,
$\textbf {F-Isoc}(\bar {C})$: therefore, ![]() $\mathbb {D}(H_C)\otimes \mathbb {Q}_p\in \textbf {F-Isoc}^{{\dagger} }(C)$. However, this yields a sub-object (in
$\mathbb {D}(H_C)\otimes \mathbb {Q}_p\in \textbf {F-Isoc}^{{\dagger} }(C)$. However, this yields a sub-object (in ![]() $\textbf {F-Isoc}^{{\dagger} }(C)$) of
$\textbf {F-Isoc}^{{\dagger} }(C)$) of ![]() $\mathbb {D}(G_C)\otimes \mathbb {Q}_p$, contradicting the absolute irreducibility of the hypothesis. Therefore,
$\mathbb {D}(G_C)\otimes \mathbb {Q}_p$, contradicting the absolute irreducibility of the hypothesis. Therefore, ![]() $G_C$ has a non-empty supersingular locus.
$G_C$ has a non-empty supersingular locus.
Now, suppose that ![]() $G_C\rightarrow C$ is not generically versally deformed, i.e. that
$G_C\rightarrow C$ is not generically versally deformed, i.e. that ![]() $KS=0$ identically on
$KS=0$ identically on ![]() $C$. Then by [Reference XiaXia13, Theorem 6.1], there is a
$C$. Then by [Reference XiaXia13, Theorem 6.1], there is a ![]() $p$-divisible group
$p$-divisible group ![]() $(G_1)_C\rightarrow C$ such that
$(G_1)_C\rightarrow C$ such that ![]() $(G_1)_C^{(p)}\cong G_C$, i.e. the Frobenius twist of
$(G_1)_C^{(p)}\cong G_C$, i.e. the Frobenius twist of ![]() $(G_1)_C$ is isomorphic to
$(G_1)_C$ is isomorphic to ![]() $G_C$. The
$G_C$. The ![]() $p$-divisible groups
$p$-divisible groups ![]() $G_C$ and
$G_C$ and ![]() $(G_1)_C$ are isogenous. If the Kodaira–Spencer map for
$(G_1)_C$ are isogenous. If the Kodaira–Spencer map for ![]() $(G_1)_C$ is non-zero, we may stop. Otherwise, we may apply [Reference XiaXia13, Theorem 6.1] again to find a
$(G_1)_C$ is non-zero, we may stop. Otherwise, we may apply [Reference XiaXia13, Theorem 6.1] again to find a ![]() $p$-divisible group
$p$-divisible group ![]() $(G_2)_C\rightarrow C$ such that
$(G_2)_C\rightarrow C$ such that ![]() $(G_2)_C^{(p)}\cong (G_1)_C$. We claim this process must terminate at some point. Here is a simple proof (also indicated in [Reference KrishnamoorthyKri22, p. 253]). Let
$(G_2)_C^{(p)}\cong (G_1)_C$. We claim this process must terminate at some point. Here is a simple proof (also indicated in [Reference KrishnamoorthyKri22, p. 253]). Let ![]() $c$ be a closed point of
$c$ be a closed point of ![]() $C$ such that
$C$ such that ![]() $G_c$ is supersingular. Then the (equal characteristic) deformation map:
$G_c$ is supersingular. Then the (equal characteristic) deformation map:
is non-zero, because ![]() $G_C$ is generically ordinary. (In other words, if
$G_C$ is generically ordinary. (In other words, if ![]() $u_c$ were
$u_c$ were ![]() $0$, then the
$0$, then the ![]() $p$-divisible group over
$p$-divisible group over ![]() $\text {Spec}(\kappa (c)[[z_c]])$ would be supersingular at both the closed and the generic point, which is a contradiction: over the generic point, the
$\text {Spec}(\kappa (c)[[z_c]])$ would be supersingular at both the closed and the generic point, which is a contradiction: over the generic point, the ![]() $p$-divisible group is base-changed from
$p$-divisible group is base-changed from ![]() $\mathbb {F}_q(C)$ along the map
$\mathbb {F}_q(C)$ along the map ![]() $\mathbb {F}_q(C)\hookrightarrow \kappa (c)[[z_c]]$.)
$\mathbb {F}_q(C)\hookrightarrow \kappa (c)[[z_c]]$.)
The map ![]() $KS_c$ is simply the derivative of
$KS_c$ is simply the derivative of ![]() $u_c$. In particular,
$u_c$. In particular, ![]() $KS_c=0$ implies that
$KS_c=0$ implies that ![]() $u_c^*(t)\in \kappa (c)[[z_c]]$ is a power series in
$u_c^*(t)\in \kappa (c)[[z_c]]$ is a power series in ![]() $z_c^p$; on the level of the universal deformation map
$z_c^p$; on the level of the universal deformation map ![]() $u_c$, Frobenius untwisting amounts to extracting a
$u_c$, Frobenius untwisting amounts to extracting a ![]() $p$th root of
$p$th root of ![]() $u_c^*(t)$. As
$u_c^*(t)$. As ![]() $u_c$ is not constant, this process must terminate.
$u_c$ is not constant, this process must terminate.
Corollary 2.5 Let the notation be as in Theorem 2.2. Further, suppose the following.
• The lisse
 ${\overline {{\mathbb {Q}}}_\ell }$-sheaf
${\overline {{\mathbb {Q}}}_\ell }$-sheaf  ${\mathbb {L}}$ has infinite, unipotent local monodromy around each point
${\mathbb {L}}$ has infinite, unipotent local monodromy around each point  $\infty \in Z$.
$\infty \in Z$.• Let
 $E$ be the field generated by Frobenius traces of
$E$ be the field generated by Frobenius traces of  ${\mathbb {L}}$. Suppose that
${\mathbb {L}}$. Suppose that  $p$ splits completely in
$p$ splits completely in  $E$.
$E$.
Then there exists an abelian scheme ![]() $f_C\colon A_C\rightarrow C$ satisfying all of the conclusions of Drinfeld's theorem 2.2, together with the further properties
$f_C\colon A_C\rightarrow C$ satisfying all of the conclusions of Drinfeld's theorem 2.2, together with the further properties
where:
(1) the
 $G_{C,i}$ are all mutually non-isogenous;
$G_{C,i}$ are all mutually non-isogenous;(2) each
 $G_{C,i}$ is a height
$G_{C,i}$ is a height  $2$, dimension
$2$, dimension  $1$
$1$  $p$-divisible group on
$p$-divisible group on  $C$; and
$C$; and(3) each
 $G_{C,i}$ is generically versally deformed, generically ordinary, and has non-empty supersingular locus.
$G_{C,i}$ is generically versally deformed, generically ordinary, and has non-empty supersingular locus.
Proof. We will first construct ![]() $\bigoplus _i G_{C,i}$ with the desired properties.
$\bigoplus _i G_{C,i}$ with the desired properties.
Let ![]() $f\colon A_C\rightarrow C$ be an abelian scheme produced by Drinfeld's theorem 2.2. By Grothendieck's monodromy criterion for semistable reduction,
$f\colon A_C\rightarrow C$ be an abelian scheme produced by Drinfeld's theorem 2.2. By Grothendieck's monodromy criterion for semistable reduction, ![]() $A_C\rightarrow C$ is totally degenerate around every point of
$A_C\rightarrow C$ is totally degenerate around every point of ![]() $Z$. The
$Z$. The ![]() $F$-isocrystal
$F$-isocrystal ![]() $\mathcal {E}:=\mathbb {D}(A_C[p^{\infty }])\otimes \mathbb {Q}_p$ is a semi-simple object of
$\mathcal {E}:=\mathbb {D}(A_C[p^{\infty }])\otimes \mathbb {Q}_p$ is a semi-simple object of ![]() $\textbf {F-Isoc}^{{\dagger} }(C)$ by [Reference PálPál22]. We claim that
$\textbf {F-Isoc}^{{\dagger} }(C)$ by [Reference PálPál22]. We claim that ![]() $\mathcal {E}$ is the companion to
$\mathcal {E}$ is the companion to ![]() $R^1(\pi _C)_*\overline {\mathbb {Q}}_{\ell }$. Indeed, a theorem of Zarhin [Reference Moret-BaillyMor85, Chapitre XII, Theorem 2.5, pp. 244–245] implies that
$R^1(\pi _C)_*\overline {\mathbb {Q}}_{\ell }$. Indeed, a theorem of Zarhin [Reference Moret-BaillyMor85, Chapitre XII, Theorem 2.5, pp. 244–245] implies that ![]() $R^1(\pi _C)_*\overline {\mathbb {Q}}_{\ell }$ is semi-simple and the characteristic polynomials of Frobenius agree at closed points by [Reference Katz and MessingKM74]. On the other hand, there is a decomposition:
$R^1(\pi _C)_*\overline {\mathbb {Q}}_{\ell }$ is semi-simple and the characteristic polynomials of Frobenius agree at closed points by [Reference Katz and MessingKM74]. On the other hand, there is a decomposition:
where ![]() $\mathcal {E}_i$ are irreducible objects of
$\mathcal {E}_i$ are irreducible objects of ![]() $\textbf {F-Isoc}^{{\dagger} }(C)_{\overline {\mathbb {Q}}_p}$.
$\textbf {F-Isoc}^{{\dagger} }(C)_{\overline {\mathbb {Q}}_p}$.
It follows from [Reference Krishnamoorthy and PálKP22, Remark 2.8] that every summand ![]() $\mathcal {E}_i$ is a companion of
$\mathcal {E}_i$ is a companion of ![]() ${\mathbb {L}}$.Footnote 9 As the relation of companions preserves ‘infinite monodromy at
${\mathbb {L}}$.Footnote 9 As the relation of companions preserves ‘infinite monodromy at ![]() $\infty \in Z$’, each
$\infty \in Z$’, each ![]() $\mathcal {E}_i$ has infinite monodromy around every
$\mathcal {E}_i$ has infinite monodromy around every ![]() $\infty \in Z$.
$\infty \in Z$.
In addition, ![]() $\det (\mathcal {E}_i)=\overline {\mathbb {Q}}_p(1)$, again because the property ‘cyclotomic determinant’ is preserved under the companions relation.
$\det (\mathcal {E}_i)=\overline {\mathbb {Q}}_p(1)$, again because the property ‘cyclotomic determinant’ is preserved under the companions relation.
As ![]() $p$ splits completely in
$p$ splits completely in ![]() $E$, it follows that
$E$, it follows that ![]() $E\otimes \mathbb {Q}_p\cong \Pi \mathbb {Q}_p$ acts on
$E\otimes \mathbb {Q}_p\cong \Pi \mathbb {Q}_p$ acts on ![]() $\mathcal {E}$, and the images of the idempotents are the
$\mathcal {E}$, and the images of the idempotents are the ![]() $\mathcal {E}_i$, i.e. the (absolutely) irreducible summands
$\mathcal {E}_i$, i.e. the (absolutely) irreducible summands ![]() $\mathcal {E}_i$ are objects of
$\mathcal {E}_i$ are objects of ![]() $\textbf {F-Isoc}^{{\dagger} }(C)$.
$\textbf {F-Isoc}^{{\dagger} }(C)$.
The slopes of each ![]() $\mathcal {E}_i$ are in between
$\mathcal {E}_i$ are in between ![]() $0$ and
$0$ and ![]() $1$. Therefore, we may apply [Reference Krishnamoorthy and PálKP21, Lemma 5.8]Footnote 10 and [Reference de JongdJ95] to see that for each
$1$. Therefore, we may apply [Reference Krishnamoorthy and PálKP21, Lemma 5.8]Footnote 10 and [Reference de JongdJ95] to see that for each ![]() $\mathcal {E}_i$, there exists a (non-canonical)
$\mathcal {E}_i$, there exists a (non-canonical) ![]() $p$-divisible group
$p$-divisible group ![]() $G_{C,i}$ with
$G_{C,i}$ with ![]() $\mathbb {D}(G_{C,i})\otimes \overline {\mathbb {Q}}_p \cong \mathcal {E}_i$. (Equivalently, note that
$\mathbb {D}(G_{C,i})\otimes \overline {\mathbb {Q}}_p \cong \mathcal {E}_i$. (Equivalently, note that ![]() $\mathcal {E}_i\in \textbf {F-Isoc}^{{\dagger} }(C)$, i.e. each
$\mathcal {E}_i\in \textbf {F-Isoc}^{{\dagger} }(C)$, i.e. each ![]() $\mathcal {E}_i$ has coefficients in
$\mathcal {E}_i$ has coefficients in ![]() $\mathbb {Q}_p$, by the hypothesis that
$\mathbb {Q}_p$, by the hypothesis that ![]() $p$ splits completely in
$p$ splits completely in ![]() $E$.)
$E$.)
The ![]() $p$-divisible groups
$p$-divisible groups ![]() $A_C[p^{\infty }]$ and
$A_C[p^{\infty }]$ and ![]() $\bigoplus _i G_{C,i}$ are isogenous. At this point, we wish to claim that each
$\bigoplus _i G_{C,i}$ are isogenous. At this point, we wish to claim that each ![]() $G_{C,i}$ has strong strict semistable reduction along
$G_{C,i}$ has strong strict semistable reduction along ![]() $Z$. First of all, note that
$Z$. First of all, note that ![]() $A_C[p^{\infty }]$ has strong strict semistable reduction by [Reference de JongdJ98, 2.5].
$A_C[p^{\infty }]$ has strong strict semistable reduction by [Reference de JongdJ98, 2.5].
As ![]() $\mathbb {D}(G_{C,i})\otimes \mathbb {Q}_p$ is overconvergent, it follows from [Reference PálPál22, Theorem 2.22] that every
$\mathbb {D}(G_{C,i})\otimes \mathbb {Q}_p$ is overconvergent, it follows from [Reference PálPál22, Theorem 2.22] that every ![]() $G_{C,i}$ has semistable reduction along
$G_{C,i}$ has semistable reduction along ![]() $Z$. Suppose for contradiction that
$Z$. Suppose for contradiction that ![]() $G_{C,1}$ extended through some cusp
$G_{C,1}$ extended through some cusp ![]() $\infty \in Z$. Then
$\infty \in Z$. Then ![]() $\mathcal {E}_1 \cong \mathbb {D}(G_{C,1})\otimes \mathbb {Q}_p$ also extends to an (overconvergent)
$\mathcal {E}_1 \cong \mathbb {D}(G_{C,1})\otimes \mathbb {Q}_p$ also extends to an (overconvergent) ![]() $F$-isocrystal on the curve
$F$-isocrystal on the curve ![]() $C\cup \{\infty \}=\bar {C}\setminus \{Z\setminus \infty \}$. As each of the
$C\cup \{\infty \}=\bar {C}\setminus \{Z\setminus \infty \}$. As each of the ![]() $\mathcal {E}_i$ are companions, this implies that they all also extend to
$\mathcal {E}_i$ are companions, this implies that they all also extend to ![]() $C\cup \{\infty \}$. Therefore, the
$C\cup \{\infty \}$. Therefore, the ![]() $\ell$-adic companion also extends to
$\ell$-adic companion also extends to ![]() $C\cup \{\infty \}$. This implies that
$C\cup \{\infty \}$. This implies that ![]() ${\mathbb {L}}$ also extends to a lisse
${\mathbb {L}}$ also extends to a lisse ![]() $\overline {\mathbb {Q}}_{\ell }$-sheaf on
$\overline {\mathbb {Q}}_{\ell }$-sheaf on ![]() $C\cup \{\infty \}$, contradicting our assumption that
$C\cup \{\infty \}$, contradicting our assumption that ![]() ${\mathbb {L}}$ had infinite, unipotent monodromy around
${\mathbb {L}}$ had infinite, unipotent monodromy around ![]() $\infty$.
$\infty$.
We may now apply Proposition 2.4 to replace each ![]() $G_{C,i}$ with an isogenous
$G_{C,i}$ with an isogenous ![]() $p$-divisible group that satisfies the two conclusions of the proposition. Note that we still have the relation
$p$-divisible group that satisfies the two conclusions of the proposition. Note that we still have the relation ![]() $A_C[p^{\infty }]$ is isogenous to
$A_C[p^{\infty }]$ is isogenous to ![]() $\bigoplus G_{C,i}$.
$\bigoplus G_{C,i}$.
By [Reference Krishnamoorthy and PálKP22, Lemma 2.13], it follows that we can replace ![]() $A_C$ by an isogenous abelian scheme such that
$A_C$ by an isogenous abelian scheme such that
where every ![]() $G_{C,i}$ is generically versally deformed, is generically ordinary, and has supersingular points. Finally, each
$G_{C,i}$ is generically versally deformed, is generically ordinary, and has supersingular points. Finally, each ![]() $G_i$ will be mutually non-isogenous because the
$G_i$ will be mutually non-isogenous because the ![]() $F$-isocrystals
$F$-isocrystals ![]() $\mathbb {D}(G_i)\otimes \mathbb {Q}_p$ are a complete collection of
$\mathbb {D}(G_i)\otimes \mathbb {Q}_p$ are a complete collection of ![]() $p$-adic companions of
$p$-adic companions of ![]() $\mathbb {L}$ (see [Reference Krishnamoorthy and PálKP22, Remark 2.8]).
$\mathbb {L}$ (see [Reference Krishnamoorthy and PálKP22, Remark 2.8]).
Using the above, we will be able to extract all of the ![]() $p$-adic information we need from Theorem 2.2 to prove Theorem 1.4. We need one final piece of notation.
$p$-adic information we need from Theorem 2.2 to prove Theorem 1.4. We need one final piece of notation.
Definition 2.6 Let ![]() $N\geq 1$ be an integer prime to
$N\geq 1$ be an integer prime to ![]() $p$ and let
$p$ and let ![]() $g\geq 1$ be a positive integer. Then
$g\geq 1$ be a positive integer. Then ![]() $\mathscr {A}_{g,1,N}/\textrm {Spec}({\mathbb {Z}}[1/N])$ denotes the (fine) moduli space of principally polarized abelian varieties with trivial full level
$\mathscr {A}_{g,1,N}/\textrm {Spec}({\mathbb {Z}}[1/N])$ denotes the (fine) moduli space of principally polarized abelian varieties with trivial full level ![]() $N$ structure. This is a smooth, quasi-projective scheme over
$N$ structure. This is a smooth, quasi-projective scheme over ![]() $\textrm {Spec}({\mathbb {Z}}[1/N])$. It has a compactification,
$\textrm {Spec}({\mathbb {Z}}[1/N])$. It has a compactification, ![]() $\mathscr {A}^*_{g,1,N}/\textrm {Spec}({\mathbb {Z}}[1/N])$.Footnote 11 This latter scheme has a natural ample line bundle, the Hodge line bundle, which we denote by
$\mathscr {A}^*_{g,1,N}/\textrm {Spec}({\mathbb {Z}}[1/N])$.Footnote 11 This latter scheme has a natural ample line bundle, the Hodge line bundle, which we denote by ![]() $\alpha$.
$\alpha$.
Then the precise output we need from Drinfeld's theorem 2.2 is given in the following lemma.
Lemma 2.7 Let the notation be as in Theorem 2.2. Suppose that ![]() $p$ splits completely in
$p$ splits completely in ![]() $E$ and
$E$ and ![]() ${\mathbb {L}}$ has infinite, unipotent monodromy around every point of
${\mathbb {L}}$ has infinite, unipotent monodromy around every point of ![]() $Z$.
$Z$.
Then there exists a principally polarized abelian scheme abelian scheme ![]() $f\colon B_C\rightarrow C$, of
$f\colon B_C\rightarrow C$, of ![]() $\mathrm {SL}_2$ type and dimension
$\mathrm {SL}_2$ type and dimension ![]() $8h$, such that
$8h$, such that ![]() ${\mathbb {L}}$ occurs as a direct summand of
${\mathbb {L}}$ occurs as a direct summand of ![]() $R^1f_*\overline {{\mathbb {Q}}}_\ell$, and the following hold.
$R^1f_*\overline {{\mathbb {Q}}}_\ell$, and the following hold.
(1) The abelian scheme
 $B_C\rightarrow C$ has semistable, infinite reduction along
$B_C\rightarrow C$ has semistable, infinite reduction along  $\bar {C}\backslash C$. Call the Néron model
$\bar {C}\backslash C$. Call the Néron model  $\bar {B}_{\bar {C}}\rightarrow \bar {C}$.
$\bar {B}_{\bar {C}}\rightarrow \bar {C}$.(2) There exist
 $h$ mutually non-isogenous
$h$ mutually non-isogenous  $p$-divisible groups
$p$-divisible groups  $G_{C,i}$, each of height
$G_{C,i}$, each of height  $2$, dimension
$2$, dimension  $1$, and generically versally deformed, such that there is a decomposition of
$1$, and generically versally deformed, such that there is a decomposition of  $p$-divisible groups
$p$-divisible groups
 \begin{align*} \displaystyle B_C[p^{\infty}]\cong \bigoplus_i (G_{C,i}\times G_{C,i}^t)^4. \end{align*}
\begin{align*} \displaystyle B_C[p^{\infty}]\cong \bigoplus_i (G_{C,i}\times G_{C,i}^t)^4. \end{align*}
(3) After Kato and Trihan, to
 $\bar {f}\colon \bar {B}_{\bar {C}}\rightarrow \bar {C}$ there is an associated logarithmic
$\bar {f}\colon \bar {B}_{\bar {C}}\rightarrow \bar {C}$ there is an associated logarithmic  $F$-crystal with nilpotent residues
$F$-crystal with nilpotent residues  $(M,F)$ in finite, locally free modules on the log pair
$(M,F)$ in finite, locally free modules on the log pair  $(\bar {C},Z)$. Similarly, there is a logarithmic Hodge vector bundle, which we write as
$(\bar {C},Z)$. Similarly, there is a logarithmic Hodge vector bundle, which we write as  $\Omega _{\bar {B}/\bar {C}}$, a rank
$\Omega _{\bar {B}/\bar {C}}$, a rank  $8h$ vector bundle on
$8h$ vector bundle on  $\bar {C}$. Then the following hold:
$\bar {C}$. Then the following hold:
(i)
 $\Omega _{\bar {B}/\bar {C}}$ splits as the direct sum of
$\Omega _{\bar {B}/\bar {C}}$ splits as the direct sum of  $8h$ positive line bundles on
$8h$ positive line bundles on  $\bar {C}$;
$\bar {C}$;(ii) the log Kodaira–Spencer map (constructed in [Reference Faltings and ChaiFC90, Ch. III, Corollary 9.8]
where \[ \theta\colon \Omega_{\bar{B}/\bar{C}}\rightarrow R^1\bar{f}_* (\mathcal{O}_{\bar{B}})\otimes \omega_{\bar{C}}(Z), \]
\[ \theta\colon \Omega_{\bar{B}/\bar{C}}\rightarrow R^1\bar{f}_* (\mathcal{O}_{\bar{B}})\otimes \omega_{\bar{C}}(Z), \]
 $\omega _{\bar {C}}$ denotes the sheaf of differential one-forms on
$\omega _{\bar {C}}$ denotes the sheaf of differential one-forms on  $\bar {C}$, is an injective map of coherent sheaves on
$\bar {C}$, is an injective map of coherent sheaves on  $\bar {C}$;
$\bar {C}$;(iii)
 $\deg (\Omega _{\bar {B}/\bar {C}}) \leq {h}/{2} \cdot (2g(\bar {C})-2 +|Z|)=4h\chi _{{\rm top}}(C)$;
$\deg (\Omega _{\bar {B}/\bar {C}}) \leq {h}/{2} \cdot (2g(\bar {C})-2 +|Z|)=4h\chi _{{\rm top}}(C)$;(iv) suppose
 $N$ is an integer, coprime to
$N$ is an integer, coprime to  $p$, such that
$p$, such that  $B_C[N]\rightarrow C$ is a split étale cover; then the induced moduli map
$B_C[N]\rightarrow C$ is a split étale cover; then the induced moduli map  $C\rightarrow \mathscr {A}_{8h,1,N}$ extends to a map
where the latter denotes the Baily–Borel compactification; then the Hodge line bundle
$C\rightarrow \mathscr {A}_{8h,1,N}$ extends to a map
where the latter denotes the Baily–Borel compactification; then the Hodge line bundle \[ \bar{C}\rightarrow \mathscr{A}^*_{8h,1,N}, \]
\[ \bar{C}\rightarrow \mathscr{A}^*_{8h,1,N}, \]
 $\alpha$ on
$\alpha$ on  $\mathscr {A}^*_{8h,1,N}$ pulls back to
$\mathscr {A}^*_{8h,1,N}$ pulls back to  $\det (\Omega _{\bar {B}/\bar {C}})$.
$\det (\Omega _{\bar {B}/\bar {C}})$.
Proof. Construct ![]() $A_C\rightarrow C$ as in Corollary 2.5. Again, by Grothendieck's criterion for semistable reduction of abelian varieties,
$A_C\rightarrow C$ as in Corollary 2.5. Again, by Grothendieck's criterion for semistable reduction of abelian varieties, ![]() $A_C\rightarrow C$ must have semistable reduction. Set
$A_C\rightarrow C$ must have semistable reduction. Set ![]() $B_C:=(A_C\times A_C^t)^4$; then by a result of Zarhin [Reference Moret-BaillyMor81, Chapitre IX, Lemme 1.1, p. 205],
$B_C:=(A_C\times A_C^t)^4$; then by a result of Zarhin [Reference Moret-BaillyMor81, Chapitre IX, Lemme 1.1, p. 205], ![]() $B_C\rightarrow C$ is principally polarized. Moreover, it clearly has semistable reduction. From the construction, and the fact that
$B_C\rightarrow C$ is principally polarized. Moreover, it clearly has semistable reduction. From the construction, and the fact that ![]() $A^t_C[p^{\infty }]\cong (A_C[p^{\infty }])^t$, where the first transpose is ‘dual abelian scheme’ and the second is ‘Serre-dual
$A^t_C[p^{\infty }]\cong (A_C[p^{\infty }])^t$, where the first transpose is ‘dual abelian scheme’ and the second is ‘Serre-dual ![]() $p$-divisible group’, it follows that part (2) holds.
$p$-divisible group’, it follows that part (2) holds.
We are left to prove part (3). To do this, we will make heavy use of [Reference Krishnamoorthy and PálKP22, Setup A.10, Proposition A.11]. First of all, each ![]() $\mathbb {D}(G_{C,i})$, a priori an Dieudonné crystal on
$\mathbb {D}(G_{C,i})$, a priori an Dieudonné crystal on ![]() $C$, extends uniquely to logarithmic Dieudonné crystal (with nilpotent residues) on
$C$, extends uniquely to logarithmic Dieudonné crystal (with nilpotent residues) on ![]() $(\bar {C},Z)$. Indeed, existence of the extension of
$(\bar {C},Z)$. Indeed, existence of the extension of ![]() $\mathbb {D}(B_C[p^{\infty }])$ follows from [Reference Kato and TrihanKT03, (4.4)–(4.8)] and uniqueness from [Reference Krishnamoorthy and PálKP22, Proposition A.11(3)]: name the extension
$\mathbb {D}(B_C[p^{\infty }])$ follows from [Reference Kato and TrihanKT03, (4.4)–(4.8)] and uniqueness from [Reference Krishnamoorthy and PálKP22, Proposition A.11(3)]: name the extension ![]() $(M,F,V)$. These two results immediately imply the desired existence and uniqueness for the extension of
$(M,F,V)$. These two results immediately imply the desired existence and uniqueness for the extension of ![]() $\mathbb {D}(G_i)$ to a logarithmic
$\mathbb {D}(G_i)$ to a logarithmic ![]() $F$-crystal, which we name
$F$-crystal, which we name ![]() $(M_i,F,V)$. The uniqueness implies that the (unique) extension of
$(M_i,F,V)$. The uniqueness implies that the (unique) extension of ![]() $\mathbb {D}(G_i^t)$ is isomorphic to the dual logarithmic Dieudnné crystal
$\mathbb {D}(G_i^t)$ is isomorphic to the dual logarithmic Dieudnné crystal ![]() $(M_i,F,V)^t$ by [Reference Krishnamoorthy and PálKP21, (5.11) and (5.12)].
$(M_i,F,V)^t$ by [Reference Krishnamoorthy and PálKP21, (5.11) and (5.12)].
Set ![]() $M_{(\bar {C},Z)}$ to be the evaluation of
$M_{(\bar {C},Z)}$ to be the evaluation of ![]() $M$ on the trivial thickening of
$M$ on the trivial thickening of ![]() $(\bar {C},Z)$ and set
$(\bar {C},Z)$ and set ![]() $\Omega$ to be the kernel of
$\Omega$ to be the kernel of ![]() $F$ on
$F$ on ![]() $M_{(\bar {C},Z)}$; then
$M_{(\bar {C},Z)}$; then ![]() $\Omega$ is a vector bundle on
$\Omega$ is a vector bundle on ![]() $\bar {C}$, called the Hodge vector bundle. (Kato and Trihan obtain the dual version of this in [Reference Kato and TrihanKT03, (5.1)], especially Lemma 5.3 of [Reference Kato and TrihanKT03].)Footnote 12 Similarly, we can construct the Hodge bundle
$\bar {C}$, called the Hodge vector bundle. (Kato and Trihan obtain the dual version of this in [Reference Kato and TrihanKT03, (5.1)], especially Lemma 5.3 of [Reference Kato and TrihanKT03].)Footnote 12 Similarly, we can construct the Hodge bundle ![]() $\Omega _i$ of each
$\Omega _i$ of each ![]() $(M_i,F)$, which will be a line bundle on
$(M_i,F)$, which will be a line bundle on ![]() $\bar {C}$. Moreover, there is a short exact sequence
$\bar {C}$. Moreover, there is a short exact sequence
where ![]() $\Psi _i$ is the Hodge bundle of
$\Psi _i$ is the Hodge bundle of ![]() $G_i^t$. We have an isomorphism of vector bundles on
$G_i^t$. We have an isomorphism of vector bundles on ![]() $\bar {C}$:
$\bar {C}$:
As each ![]() $G_{C,i}$ has non-empty supersingular locus, it follows that the Hasse invariant associated to
$G_{C,i}$ has non-empty supersingular locus, it follows that the Hasse invariant associated to ![]() $G_{C,i}$,
$G_{C,i}$,
is non-zero, which implies that ![]() $\Omega _i$ is a positive degree line bundle on
$\Omega _i$ is a positive degree line bundle on ![]() $\bar {C}$. As
$\bar {C}$. As ![]() $G_{C,i}^t$ is supersingular exactly when
$G_{C,i}^t$ is supersingular exactly when ![]() $G_{C,i}$ is supersingular, we deduce that
$G_{C,i}$ is supersingular, we deduce that ![]() $\Psi _i$ is also positive. Therefore,
$\Psi _i$ is also positive. Therefore, ![]() $\Omega =\Omega _{\bar {B}/\bar {C}}$ splits as the direct sum of
$\Omega =\Omega _{\bar {B}/\bar {C}}$ splits as the direct sum of ![]() $8h$ positive line bundles. In particular, we have shown part (i). We further note that
$8h$ positive line bundles. In particular, we have shown part (i). We further note that ![]() $\Omega$ is isomorphic to the Hodge line bundle associated to the Néron model of
$\Omega$ is isomorphic to the Hodge line bundle associated to the Néron model of ![]() $B_C\rightarrow C$ by [Reference Krishnamoorthy and PálKP22, (A.11)] (this was first proven in [Reference Kato and TrihanKT03]).
$B_C\rightarrow C$ by [Reference Krishnamoorthy and PálKP22, (A.11)] (this was first proven in [Reference Kato and TrihanKT03]).
For the next step, Faltings and Chai have constructed the following Kodaira–Spencer map [Reference Faltings and ChaiFC90, Ch. III, Corollary 9.8]:
extending the usual Kodaira–Spencer map over ![]() $C$. As
$C$. As ![]() $B$ admits a principal polarization, we have that
$B$ admits a principal polarization, we have that ![]() $B_C\cong B^t_C$ and, hence,
$B_C\cong B^t_C$ and, hence, ![]() $\bar {B}_{\bar {C}}\cong \bar {B^t}_{\bar {C}}$, as both are simply the respective Néron models. Therefore, we may equivalently write (2.2) as
$\bar {B}_{\bar {C}}\cong \bar {B^t}_{\bar {C}}$, as both are simply the respective Néron models. Therefore, we may equivalently write (2.2) as
Under the decomposition
and after restricting to ![]() $C$, the above
$C$, the above ![]() $\theta |_C$ is just the sum of the Kodaira–Spencer maps for each
$\theta |_C$ is just the sum of the Kodaira–Spencer maps for each ![]() $G_i$ and
$G_i$ and ![]() $G_i^t$:
$G_i^t$:
These were constructed to be non-zero, as both ![]() $G_i$ and
$G_i$ and ![]() $G_i^t$ are generically versally deformed; therefore, the Kodaira–Spencer map of sheaves is an injective map of coherent sheaves. Therefore, part (ii) is shown.
$G_i^t$ are generically versally deformed; therefore, the Kodaira–Spencer map of sheaves is an injective map of coherent sheaves. Therefore, part (ii) is shown.
Fortunately, part (iii) is an easy corollary of part (ii). Indeed, taking degrees, we see that
from which the inequality follows immediately.
Finally, let us prove part (iv). By moduli theory, we have a map ![]() $C\rightarrow \mathscr {A}_{8h,1,N}$, where the latter is a fine moduli scheme. As
$C\rightarrow \mathscr {A}_{8h,1,N}$, where the latter is a fine moduli scheme. As ![]() $\bar {C}$ is a smooth curve and the Baily–Borel compactification
$\bar {C}$ is a smooth curve and the Baily–Borel compactification ![]() $\mathscr {A}^*_{8h,1,N}$ is proper, it follows that we get an extension:
$\mathscr {A}^*_{8h,1,N}$ is proper, it follows that we get an extension:
Finally, the argument that the Hodge line bundle on ![]() $\mathscr {A}^*_{8h,1,N}$ pulls back under
$\mathscr {A}^*_{8h,1,N}$ pulls back under ![]() $\lambda$ to
$\lambda$ to ![]() $\det (\Omega _{\bar {B}/\bar {C}})$ is given in the text surrounding [Reference Krishnamoorthy and PálKP22, (3.4), (3.5)]. (While the argument in [Reference Krishnamoorthy and PálKP22] is only written for
$\det (\Omega _{\bar {B}/\bar {C}})$ is given in the text surrounding [Reference Krishnamoorthy and PálKP22, (3.4), (3.5)]. (While the argument in [Reference Krishnamoorthy and PálKP22] is only written for ![]() $N=\ell$, it generalizes verbatim to the matter at hand. Indeed, the argument is an easy corollary of [Reference Faltings and ChaiFC90, Ch. V, Theorem 2.5].)
$N=\ell$, it generalizes verbatim to the matter at hand. Indeed, the argument is an easy corollary of [Reference Faltings and ChaiFC90, Ch. V, Theorem 2.5].)
3. The moduli spaces
We work in the following situation. Let ![]() $K$ be number field, let
$K$ be number field, let ![]() $N\geq 1$, set
$N\geq 1$, set ![]() $S:=\textrm {Spec}({\mathcal {O}_K[1/N]})$, and let
$S:=\textrm {Spec}({\mathcal {O}_K[1/N]})$, and let ![]() ${\mathfrak {X}}/S$ be a smooth projective curve, let
${\mathfrak {X}}/S$ be a smooth projective curve, let ![]() ${\mathfrak D}\subset {\mathfrak {X}}$ be a relative reduced divisor, and let
${\mathfrak D}\subset {\mathfrak {X}}$ be a relative reduced divisor, and let ![]() ${\mathfrak {U}}$ denote the open complement.
${\mathfrak {U}}$ denote the open complement.
Let ![]() $\ell$ be a prime number and let
$\ell$ be a prime number and let ![]() $g\geq 1$ be an integer. We again denote by
$g\geq 1$ be an integer. We again denote by ![]() $\mathscr {A}^*_{g,1,\ell ^3}$ the Baily–Borel compactification of
$\mathscr {A}^*_{g,1,\ell ^3}$ the Baily–Borel compactification of ![]() $\mathscr {A}_{g,1,\ell ^3}$, which is defined over
$\mathscr {A}_{g,1,\ell ^3}$, which is defined over ![]() $\textrm {Spec}(\mathbb {Z}[1/\ell ])$. This moduli space has a natural ample line bundle, the Hodge line bundle, which we denote by
$\textrm {Spec}(\mathbb {Z}[1/\ell ])$. This moduli space has a natural ample line bundle, the Hodge line bundle, which we denote by ![]() $\alpha$.
$\alpha$.
Definition 3.1 Fix a positive integer ![]() $b$. Denote by
$b$. Denote by ![]() $\mathcal {H}$ the following contravariant pseudo-functor from the category of
$\mathcal {H}$ the following contravariant pseudo-functor from the category of ![]() $S$ schemes to the 2-category of groupoids. The value
$S$ schemes to the 2-category of groupoids. The value ![]() $\mathcal {H}(T)$ for an
$\mathcal {H}(T)$ for an ![]() $S$-scheme
$S$-scheme ![]() $T$ is the groupoid of triples
$T$ is the groupoid of triples ![]() $({\mathfrak Y},\varphi,\lambda )$, that fit into a diagram
$({\mathfrak Y},\varphi,\lambda )$, that fit into a diagram

where
•
 ${\mathfrak Y}/T$ is a smooth, projective, geometrically connected curve;
${\mathfrak Y}/T$ is a smooth, projective, geometrically connected curve;•
 $\lambda$ sends
$\lambda$ sends  ${\mathfrak W}:=\varphi ^{-1}({\mathfrak {U}})\subset {\mathfrak Y}$ to
${\mathfrak W}:=\varphi ^{-1}({\mathfrak {U}})\subset {\mathfrak Y}$ to  $\mathscr {A}_{g,1,\ell ^3}\times T\subset \mathscr {A}_{g,1,\ell ^3}^*\times T$;
$\mathscr {A}_{g,1,\ell ^3}\times T\subset \mathscr {A}_{g,1,\ell ^3}^*\times T$;•
 $\varphi$ is finite morphism, of degree
$\varphi$ is finite morphism, of degree  $\leq |\mathrm {GL}_{2g}({\mathbb {Z}}/\ell ^3{\mathbb {Z}})|$, and étale over
$\leq |\mathrm {GL}_{2g}({\mathbb {Z}}/\ell ^3{\mathbb {Z}})|$, and étale over  ${\mathfrak {U}}$;
${\mathfrak {U}}$;• there exists some cusp
 $\infty$ of
$\infty$ of  ${\mathfrak Y}(T)$ (lying over a point of
${\mathfrak Y}(T)$ (lying over a point of  ${\mathfrak D}(T)$ of
${\mathfrak D}(T)$ of  ${\mathfrak {X}}(T)$) that is sent to a 0-dimensional cusp of
${\mathfrak {X}}(T)$) that is sent to a 0-dimensional cusp of  $\mathscr {A}^*_{g,1,\ell ^3}\times T$; and
$\mathscr {A}^*_{g,1,\ell ^3}\times T$; and• the degree of the pulled-back Hodge line bundle
 $\lambda ^*(\alpha )$ on every geometric fiber of
$\lambda ^*(\alpha )$ on every geometric fiber of  ${\mathfrak Y}$ is
${\mathfrak Y}$ is  $\leq b$;
$\leq b$;
with the natural notion of isomorphism that if ![]() $({\mathfrak Y},\varphi,\lambda )$ and
$({\mathfrak Y},\varphi,\lambda )$ and ![]() $({\mathfrak Y}',\varphi ',\lambda ')$ are elements of
$({\mathfrak Y}',\varphi ',\lambda ')$ are elements of ![]() $\mathcal {H}(T)$, then an isomorphism between them is an
$\mathcal {H}(T)$, then an isomorphism between them is an ![]() ${\mathfrak {X}}_T$-isomorphism
${\mathfrak {X}}_T$-isomorphism ![]() ${\mathfrak Y}\rightarrow {\mathfrak Y}'$ that intertwines
${\mathfrak Y}\rightarrow {\mathfrak Y}'$ that intertwines ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi '$ as well as
$\varphi '$ as well as ![]() $\lambda$ and
$\lambda$ and ![]() $\lambda '$.
$\lambda '$.
Colloquially, the functor ![]() $\mathcal {H}$ parameterizes finite covers
$\mathcal {H}$ parameterizes finite covers ![]() ${\mathfrak Y}$ of
${\mathfrak Y}$ of ![]() ${\mathfrak {X}}$ equipped with a (principally polarized) abelian scheme of dimension
${\mathfrak {X}}$ equipped with a (principally polarized) abelian scheme of dimension ![]() $g$ with trivial
$g$ with trivial ![]() $\ell ^3$ level structure, such that the induced map
$\ell ^3$ level structure, such that the induced map ![]() ${\mathfrak Y}\rightarrow \mathscr {A}^*_{g,1,\ell ^3}$ has ‘degree’ bounded by
${\mathfrak Y}\rightarrow \mathscr {A}^*_{g,1,\ell ^3}$ has ‘degree’ bounded by ![]() $b$.
$b$.
Proposition 3.2 After potentially increasing ![]() $N$ (equivalently, replacing
$N$ (equivalently, replacing ![]() $S$ by a non-empty open subscheme), the functor
$S$ by a non-empty open subscheme), the functor ![]() $\mathcal {H}$ is represented by a finite-type Deligne–Mumford stack over
$\mathcal {H}$ is represented by a finite-type Deligne–Mumford stack over ![]() $S$.
$S$.
Proof. By increasing ![]() $N$, we can assume that all covers
$N$, we can assume that all covers ![]() $\varphi \colon {\mathfrak Y}\rightarrow {\mathfrak {X}}$ that occur in the definition of
$\varphi \colon {\mathfrak Y}\rightarrow {\mathfrak {X}}$ that occur in the definition of ![]() $\mathcal {H}$ are tamely ramified at the cusps. More precisely, this will hold for any
$\mathcal {H}$ are tamely ramified at the cusps. More precisely, this will hold for any ![]() $N>|\text {GL}_{2g}(\mathbb {Z}/\ell ^3\mathbb {Z})|$.
$N>|\text {GL}_{2g}(\mathbb {Z}/\ell ^3\mathbb {Z})|$.
It follows from the theory of the Hilbert scheme that for any noetherian scheme ![]() $T$ and for any relative smooth proper curve
$T$ and for any relative smooth proper curve ![]() ${\mathfrak Y}/T$ with geometrically connected fibers, the functor
${\mathfrak Y}/T$ with geometrically connected fibers, the functor ![]() $\text {Hom}^{\leq b}_T({\mathfrak Y},\mathscr {A}^*_{g,1,\ell ^3})$ parametrizing maps
$\text {Hom}^{\leq b}_T({\mathfrak Y},\mathscr {A}^*_{g,1,\ell ^3})$ parametrizing maps ![]() $\lambda$ such that the
$\lambda$ such that the ![]() $\deg (\lambda ^*(\alpha ))\leq b$ for every geometric fiber is represented by a finite-type
$\deg (\lambda ^*(\alpha ))\leq b$ for every geometric fiber is represented by a finite-type ![]() $T$-scheme. (In particular, this holds true even if
$T$-scheme. (In particular, this holds true even if ![]() $T$ is not connected and the genus of the fibers varies on different connected components.) It follows that if
$T$ is not connected and the genus of the fibers varies on different connected components.) It follows that if ![]() $T$ is a Deligne–Mumford stack, of finite type over
$T$ is a Deligne–Mumford stack, of finite type over ![]() $S$, and
$S$, and ![]() ${\mathfrak Y}/T$ is a smooth, proper curve with geometrically connected fibers, then the same functor
${\mathfrak Y}/T$ is a smooth, proper curve with geometrically connected fibers, then the same functor ![]() $\text {Hom}^{\leq b}_T({\mathfrak Y},\mathscr {A}^*_{g,1,\ell ^3})$ is represented by a finite-type Deligne–Mumford stack over
$\text {Hom}^{\leq b}_T({\mathfrak Y},\mathscr {A}^*_{g,1,\ell ^3})$ is represented by a finite-type Deligne–Mumford stack over ![]() $T$.
$T$.
On the other hand, the theory of the Hurwitz scheme implies that the functor ![]() $\text {Cov}^{c}_{({\mathfrak {X}},{\mathfrak D})/S}$ parametrizing finite tame covers
$\text {Cov}^{c}_{({\mathfrak {X}},{\mathfrak D})/S}$ parametrizing finite tame covers ![]() ${\mathfrak Y}\rightarrow {\mathfrak {X}}$ of degree
${\mathfrak Y}\rightarrow {\mathfrak {X}}$ of degree ![]() $\leq c$ such that:
$\leq c$ such that:
•
 ${\mathfrak Y}/S$ has geometrically connected fibers; and
${\mathfrak Y}/S$ has geometrically connected fibers; and•
 ${\mathfrak Y}\rightarrow {\mathfrak {X}}$ is étale over
${\mathfrak Y}\rightarrow {\mathfrak {X}}$ is étale over  ${\mathfrak {U}}:={\mathfrak {X}}\setminus {\mathfrak D}$
${\mathfrak {U}}:={\mathfrak {X}}\setminus {\mathfrak D}$
is represented by a finite-type Deligne–Mumford stack over ![]() $S$.
$S$.
There is a natural map
which is the map that sends a cover ![]() ${\mathfrak Y}\rightarrow {\mathfrak {X}}$ to the underlying curve
${\mathfrak Y}\rightarrow {\mathfrak {X}}$ to the underlying curve ![]() ${\mathfrak Y}$. Here, the notation
${\mathfrak Y}$. Here, the notation ![]() $\mathscr {M}_{k}$ stands for the moduli space of genus
$\mathscr {M}_{k}$ stands for the moduli space of genus ![]() $k$ curves. Denote by
$k$ curves. Denote by ![]() $\mathscr {C}_k\rightarrow \mathscr {M}_k$ the universal curve and by
$\mathscr {C}_k\rightarrow \mathscr {M}_k$ the universal curve and by ![]() $\mathscr {C}:=\bigsqcup \mathscr {C}_k$, which has a natural map
$\mathscr {C}:=\bigsqcup \mathscr {C}_k$, which has a natural map ![]() $\mathscr {C}\rightarrow \mathscr {M}$.
$\mathscr {C}\rightarrow \mathscr {M}$.
Then consider ![]() $\mathscr {H}$, the open substack of the 2-fiber product:
$\mathscr {H}$, the open substack of the 2-fiber product:
which corresponds to the condition that sends ![]() $\lambda (\varphi ^{-1}({\mathfrak {U}}))\subset \mathscr {A}_{g,1,\ell ^3}$, i.e. that
$\lambda (\varphi ^{-1}({\mathfrak {U}}))\subset \mathscr {A}_{g,1,\ell ^3}$, i.e. that ![]() $\varphi ^{-1}({\mathfrak {U}})$ is sent inside of the moduli space of abelian varieties. It follows that
$\varphi ^{-1}({\mathfrak {U}})$ is sent inside of the moduli space of abelian varieties. It follows that ![]() $\mathscr {H}$ is finite-type Deligne–Mumford stack over
$\mathscr {H}$ is finite-type Deligne–Mumford stack over ![]() $S$. By further imposing the condition that the map
$S$. By further imposing the condition that the map ![]() $\lambda$ sends at least one point in the boundary divisor to a zero-dimensional cusp of the Baily–Borel compactification,
$\lambda$ sends at least one point in the boundary divisor to a zero-dimensional cusp of the Baily–Borel compactification, ![]() $\mathcal {H}$ is a closed substack of
$\mathcal {H}$ is a closed substack of ![]() $\mathscr {H}$, which is again finite type.
$\mathscr {H}$, which is again finite type.
Now, let ![]() ${\mathbb {L}}$ be a lisse
${\mathbb {L}}$ be a lisse ![]() $\overline {\mathbb {Q}}_{\ell }$-sheaf as in Theorem 1.4. There exists an
$\overline {\mathbb {Q}}_{\ell }$-sheaf as in Theorem 1.4. There exists an ![]() $\ell$-adic local field
$\ell$-adic local field ![]() $M/\mathbb {Q}_{\ell }$ such that the associated representation factors through the ring of integers
$M/\mathbb {Q}_{\ell }$ such that the associated representation factors through the ring of integers ![]() $\mathcal {O}_M$:
$\mathcal {O}_M$:
Abusing notation, we call the induced lisse ![]() $\mathcal {O}_M$-sheaf
$\mathcal {O}_M$-sheaf ![]() $\mathcal {L}$. Denote by
$\mathcal {L}$. Denote by ![]() $\pi _M$ the uniformizer of
$\pi _M$ the uniformizer of ![]() $M$ and
$M$ and ![]() $\kappa _M$ the residue field of
$\kappa _M$ the residue field of ![]() $M$.
$M$.
Definition 3.3 Fix ![]() $i\geq 1$ and a lattice
$i\geq 1$ and a lattice ![]() $\mathcal {L}$ as above. Let
$\mathcal {L}$ as above. Let ![]() $\tilde {\mathcal {H}}_{i}$ denote the following contravariant pseudo-functor from
$\tilde {\mathcal {H}}_{i}$ denote the following contravariant pseudo-functor from ![]() $S$-schemes to groupoids: the value
$S$-schemes to groupoids: the value ![]() $\tilde {\mathcal {H}}_i(T)$ on an
$\tilde {\mathcal {H}}_i(T)$ on an ![]() $S$-scheme
$S$-scheme ![]() $T$ is the collection of quadruples
$T$ is the collection of quadruples ![]() $({\mathfrak Y},\varphi,\lambda, \psi )$, where
$({\mathfrak Y},\varphi,\lambda, \psi )$, where ![]() $({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}(T)$, and
$({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}(T)$, and ![]() $\psi$ is the following extra piece of data. As
$\psi$ is the following extra piece of data. As ![]() $\lambda \colon {\mathfrak W}:=\varphi ^{-1}({\mathfrak {U}})\rightarrow \mathscr {A}_{g,1,\ell ^3}$, there is a principally polarized abelian scheme
$\lambda \colon {\mathfrak W}:=\varphi ^{-1}({\mathfrak {U}})\rightarrow \mathscr {A}_{g,1,\ell ^3}$, there is a principally polarized abelian scheme ![]() $f\colon A_{{\mathfrak W}}\rightarrow {\mathfrak W}$ (with trivial
$f\colon A_{{\mathfrak W}}\rightarrow {\mathfrak W}$ (with trivial ![]() $\ell ^3$-torsion). Then
$\ell ^3$-torsion). Then
is a map of étale torsion sheaves on ![]() ${\mathfrak W}$ whose reduction modulo
${\mathfrak W}$ whose reduction modulo ![]() $\pi _M$-reduction is non-zero. In other words,
$\pi _M$-reduction is non-zero. In other words, ![]() $\mathrm {im}(\psi )\not \subseteq \pi _M(R^1f_*\mathcal {O}_M/\pi _M^i)$. There is an obvious notion of isomorphism of two such quadruples.
$\mathrm {im}(\psi )\not \subseteq \pi _M(R^1f_*\mathcal {O}_M/\pi _M^i)$. There is an obvious notion of isomorphism of two such quadruples.
The pseudo-functor ![]() $\tilde {\mathcal {H}}_i$ is actually a stack in the étale topology. This follows from the following two properties. Let
$\tilde {\mathcal {H}}_i$ is actually a stack in the étale topology. This follows from the following two properties. Let ![]() $T$ be a scheme.
$T$ be a scheme.
• There exists an internal Hom in the category of torsion locally constant abelian étale sheaves on
 $T$.
$T$.• If
 $\psi \colon \mathcal {F}\rightarrow \mathcal {G}$ is a map of torsion, locally constant étale sheaves of
$\psi \colon \mathcal {F}\rightarrow \mathcal {G}$ is a map of torsion, locally constant étale sheaves of  $\mathcal {O}_M$ modules on
$\mathcal {O}_M$ modules on  $T$, then the property that
$T$, then the property that  $\psi (\mathcal {F})\not \subset \pi _M(\mathcal {G})$ may be checked on an étale cover.
$\psi (\mathcal {F})\not \subset \pi _M(\mathcal {G})$ may be checked on an étale cover.
There are natural transformations of pseudo-functors ![]() $\tilde {\mathcal {H}}_{j}\rightarrow \tilde {\mathcal {H}}_{i}$ for any
$\tilde {\mathcal {H}}_{j}\rightarrow \tilde {\mathcal {H}}_{i}$ for any ![]() $j>i$. We claim that
$j>i$. We claim that ![]() $\tilde {\mathcal {H}}_i$ represents a finite-type Deligne–Mumford stack over
$\tilde {\mathcal {H}}_i$ represents a finite-type Deligne–Mumford stack over ![]() $S$. To prove this, it suffices to prove that the natural transformation of pseudo-functors
$S$. To prove this, it suffices to prove that the natural transformation of pseudo-functors ![]() $\tilde {\mathcal {H}}_i\rightarrow \mathcal {H}$ is representable by a scheme.
$\tilde {\mathcal {H}}_i\rightarrow \mathcal {H}$ is representable by a scheme.
Let ![]() $T$ be an
$T$ be an ![]() $S$-scheme, and
$S$-scheme, and ![]() $t:=({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}(T)$. Then we have the following pullback square.
$t:=({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}(T)$. Then we have the following pullback square.

Then ![]() $T\times _{\mathcal {H}}\tilde {\mathcal {H}}_i$ has the following description. There are two natural
$T\times _{\mathcal {H}}\tilde {\mathcal {H}}_i$ has the following description. There are two natural ![]() $\ell ^i$-torsion étale sheaves on
$\ell ^i$-torsion étale sheaves on ![]() ${\mathfrak Y}$:
${\mathfrak Y}$: ![]() $\varphi ^*(\mathcal {L}/\ell ^i)$ (which has
$\varphi ^*(\mathcal {L}/\ell ^i)$ (which has ![]() $\mathcal {O}_M/\ell ^i$-rank 2), and
$\mathcal {O}_M/\ell ^i$-rank 2), and ![]() $R^1f_*\mathcal {O}_M/\ell ^i$ (which has
$R^1f_*\mathcal {O}_M/\ell ^i$ (which has ![]() $\mathcal {O}_M/\ell ^i$-rank
$\mathcal {O}_M/\ell ^i$-rank ![]() $2g$). Then
$2g$). Then ![]() $T\times _{\mathcal {H}}\tilde {\mathcal {H}}_i$ corresponds to the (finite) set of injective maps of sheaves of abelian groups:
$T\times _{\mathcal {H}}\tilde {\mathcal {H}}_i$ corresponds to the (finite) set of injective maps of sheaves of abelian groups: ![]() $\psi \colon \varphi ^{*}(\mathcal {L}/\ell ^i)\hookrightarrow R^1f_*\mathcal {O}_M/\ell ^i$. This finite set is canonically a scheme. It follows that
$\psi \colon \varphi ^{*}(\mathcal {L}/\ell ^i)\hookrightarrow R^1f_*\mathcal {O}_M/\ell ^i$. This finite set is canonically a scheme. It follows that ![]() $\tilde {\mathcal {H}}_i\rightarrow \mathcal {H}$ is relatively representable, and hence
$\tilde {\mathcal {H}}_i\rightarrow \mathcal {H}$ is relatively representable, and hence ![]() $\tilde {\mathcal {H}}_i$ is represented by a Deligne–Mumford stack of finite type over
$\tilde {\mathcal {H}}_i$ is represented by a Deligne–Mumford stack of finite type over ![]() $S$.
$S$.
Proposition 3.4 The natural map ‘forget ![]() $\psi$’:
$\psi$’: ![]() $\tilde {\mathcal {H}_i}\rightarrow \mathcal {H}$ is finite.
$\tilde {\mathcal {H}_i}\rightarrow \mathcal {H}$ is finite.
Proof. It is obviously quasi-finite because, as argued above, if we fix ![]() $i$, then there are only finitely many choices for
$i$, then there are only finitely many choices for ![]() $\psi$. To prove it is finite, we show that it is proper.
$\psi$. To prove it is finite, we show that it is proper.
As both ![]() $\tilde {\mathcal {H}}_i$ and
$\tilde {\mathcal {H}}_i$ and ![]() $\mathcal {H}$ are of finite type over
$\mathcal {H}$ are of finite type over ![]() $S=\textrm {Spec}({\mathcal {O}_K[1/N]})$, it suffices to simply check the valuative criterion for properness. Let
$S=\textrm {Spec}({\mathcal {O}_K[1/N]})$, it suffices to simply check the valuative criterion for properness. Let ![]() $R$ be a discrete valuation ring with fraction field
$R$ be a discrete valuation ring with fraction field ![]() $F$. Suppose we have
$F$. Suppose we have ![]() $({\mathfrak Y},\varphi,\lambda ) \in \mathcal {H}(R)$ and
$({\mathfrak Y},\varphi,\lambda ) \in \mathcal {H}(R)$ and ![]() $({\mathfrak Y}_F,\varphi _F,\lambda _F,\psi _F)\in \tilde {\mathcal {H}}_i(F)$. Therefore, we have a principally polarized abelian scheme
$({\mathfrak Y}_F,\varphi _F,\lambda _F,\psi _F)\in \tilde {\mathcal {H}}_i(F)$. Therefore, we have a principally polarized abelian scheme ![]() $f'\colon A_{{\mathfrak W}}\rightarrow {\mathfrak W}$ (of dimension
$f'\colon A_{{\mathfrak W}}\rightarrow {\mathfrak W}$ (of dimension ![]() $g$, with trivial
$g$, with trivial ![]() $\ell ^3$ torsion), together with a map of torsion étale sheaves over
$\ell ^3$ torsion), together with a map of torsion étale sheaves over ![]() ${\mathfrak W}_F$ whose reduction modulo
${\mathfrak W}_F$ whose reduction modulo ![]() $\pi _M$ is non-trivial:
$\pi _M$ is non-trivial:
Note the following. If one has two finite étale sheaves on an irreducible normal scheme, and a morphism between them over the generic point, then that morphism uniquely extends to the whole scheme. (Here, we are closely following [Reference Snowden and TsimermanST18, Proof of Lemma 23].) Therefore, ![]() $\psi _F$ extends to a
$\psi _F$ extends to a ![]() $\psi$ on all of
$\psi$ on all of ![]() ${\mathfrak {U}}'_R$, and we have verified the valuative criterion for properness.
${\mathfrak {U}}'_R$, and we have verified the valuative criterion for properness.
Definition 3.5 For ![]() $i\geq 1$, set
$i\geq 1$, set
As ![]() $\tilde {\mathcal {H}}_i\rightarrow \mathcal {H}$ is relatively representable and finite (Proposition 3.4), it is universally closed. Therefore,
$\tilde {\mathcal {H}}_i\rightarrow \mathcal {H}$ is relatively representable and finite (Proposition 3.4), it is universally closed. Therefore, ![]() $\mathcal {H}_i$ is a closed subset of
$\mathcal {H}_i$ is a closed subset of ![]() $|\mathcal {H}|$, which we may equip with the induced reduced substack structure [Sta22, Tag 0508]. According the natural transformations
$|\mathcal {H}|$, which we may equip with the induced reduced substack structure [Sta22, Tag 0508]. According the natural transformations ![]() $\tilde {\mathcal {H}}_{j}\rightarrow \tilde {\mathcal {H}}_{i}$, the sequence of closed subsets are descending. Set
$\tilde {\mathcal {H}}_{j}\rightarrow \tilde {\mathcal {H}}_{i}$, the sequence of closed subsets are descending. Set
which is also equipped with the reduced induced substack structure. Then ![]() $\mathcal {H}_i$ and
$\mathcal {H}_i$ and ![]() $\mathcal {H}_{\infty }$ are Deligne–Mumford stacks of finite type over
$\mathcal {H}_{\infty }$ are Deligne–Mumford stacks of finite type over ![]() $S=\textrm {Spec}({\mathcal {O}_K[1/N]})$ for all
$S=\textrm {Spec}({\mathcal {O}_K[1/N]})$ for all ![]() $i\geq 1$.
$i\geq 1$.
Lemma 3.6 Let ![]() $T$ be an
$T$ be an ![]() $S$-scheme and let
$S$-scheme and let ![]() $({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}(T)$. Then the following conditions are equivalent:
$({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}(T)$. Then the following conditions are equivalent:
(1)
 $({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}_\infty (T)$;
$({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}_\infty (T)$;(2) there exists an injection
of lisse \[ \varphi^*(\mathcal{L})\hookrightarrow R^1f_*\mathcal{O}_M \]
\[ \varphi^*(\mathcal{L})\hookrightarrow R^1f_*\mathcal{O}_M \]
 $\mathcal {O}_M$-sheaves on
$\mathcal {O}_M$-sheaves on  $T$;
$T$;(3) there is an injection
 $\tau \colon \varphi ^*(\mathcal {L}\otimes M)\hookrightarrow R^1f_*M$ of lisse
$\tau \colon \varphi ^*(\mathcal {L}\otimes M)\hookrightarrow R^1f_*M$ of lisse  $M$-sheaves on
$M$-sheaves on  $T$.
$T$.
Proof. (2) ![]() $\Rightarrow$ (3) By applying
$\Rightarrow$ (3) By applying ![]() $- \otimes _{\mathcal {O}_M} M$ to the injection
$- \otimes _{\mathcal {O}_M} M$ to the injection ![]() $\varphi ^*(\mathcal {L})\hookrightarrow R^1f_*\mathcal {O}_M$ , we get the desired injection. (Note that both are lisse
$\varphi ^*(\mathcal {L})\hookrightarrow R^1f_*\mathcal {O}_M$ , we get the desired injection. (Note that both are lisse ![]() $\mathcal {O}_M$-sheaves, so tensoring with
$\mathcal {O}_M$-sheaves, so tensoring with ![]() $M$ yields an injective map.)
$M$ yields an injective map.)
(3) ![]() $\Rightarrow$ (2) Since
$\Rightarrow$ (2) Since ![]() $R^1f_*\mathcal {O}_M$ (respectively,
$R^1f_*\mathcal {O}_M$ (respectively, ![]() $\mathcal {L}$) is an
$\mathcal {L}$) is an ![]() $\mathcal {O}_M$-lattice in
$\mathcal {O}_M$-lattice in ![]() $R^1f_*M$ (respectively,
$R^1f_*M$ (respectively, ![]() $\mathcal {L}\otimes M$), there exists some integer
$\mathcal {L}\otimes M$), there exists some integer ![]() $\iota$ such that
$\iota$ such that
Then the map ![]() $\pi _M^\iota \tau$ is an injection from
$\pi _M^\iota \tau$ is an injection from ![]() $\varphi ^*(\mathcal {L})$ to
$\varphi ^*(\mathcal {L})$ to ![]() $R^1f_*\mathcal {O}_M$.
$R^1f_*\mathcal {O}_M$.
(2) ![]() $\Rightarrow$ (1) Denote by
$\Rightarrow$ (1) Denote by ![]() $\psi '$ the injection in condition (2). It is clear there exists some integer
$\psi '$ the injection in condition (2). It is clear there exists some integer ![]() $\lambda$ such that
$\lambda$ such that
Denote ![]() $\psi = {\psi '}/{\pi _M^\lambda }$ which is clearly an injection from
$\psi = {\psi '}/{\pi _M^\lambda }$ which is clearly an injection from ![]() $\varphi ^*(\mathcal {L})$ to
$\varphi ^*(\mathcal {L})$ to ![]() $R^1f_*\mathcal {O}_M$ and satisfies
$R^1f_*\mathcal {O}_M$ and satisfies
This is equivalent to saying that the reduction modulo ![]() $\pi _M$ of
$\pi _M$ of ![]() $\psi$ is nontrivial. Denote
$\psi$ is nontrivial. Denote ![]() $\psi _i = \psi \ {\rm mod}\ (\pi _M^i)$ for each
$\psi _i = \psi \ {\rm mod}\ (\pi _M^i)$ for each ![]() $i>0$,
$i>0$,
Since ![]() $\psi _i\ {\rm mod}\ (\pi _M) = \psi \ {\rm mod}\ (\pi _M) \neq 0$, the quadruple
$\psi _i\ {\rm mod}\ (\pi _M) = \psi \ {\rm mod}\ (\pi _M) \neq 0$, the quadruple ![]() $({\mathfrak Y},\varphi,\lambda,\psi _i)\in \tilde {\mathcal {H}}_i$. Thus,
$({\mathfrak Y},\varphi,\lambda,\psi _i)\in \tilde {\mathcal {H}}_i$. Thus, ![]() $({\mathfrak Y},\varphi,\lambda )\in \cap _{i=1}^\infty \mathcal {H}_i = \mathcal {H}_\infty$.
$({\mathfrak Y},\varphi,\lambda )\in \cap _{i=1}^\infty \mathcal {H}_i = \mathcal {H}_\infty$.
(1) ![]() $\Rightarrow$ (3) (This is the main content of the lemma.) Since
$\Rightarrow$ (3) (This is the main content of the lemma.) Since ![]() $({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}_\infty (T)$, for each
$({\mathfrak Y},\varphi,\lambda )\in \mathcal {H}_\infty (T)$, for each ![]() $i>0$, there exists a map
$i>0$, there exists a map
which is non-trivial modulo ![]() $\pi _M$. In general, the
$\pi _M$. In general, the ![]() $\psi '_i$'s do not form a compatible sequence, i.e. it is possible that there exists
$\psi '_i$'s do not form a compatible sequence, i.e. it is possible that there exists ![]() $j>i$ with the following property:
$j>i$ with the following property: ![]() $\psi '_{j}\ {\rm mod}\ {(\pi _M^i\!)} \not \equiv \psi '_i$. Therefore, one cannot directly take projective limits to find our desired map
$\psi '_{j}\ {\rm mod}\ {(\pi _M^i\!)} \not \equiv \psi '_i$. Therefore, one cannot directly take projective limits to find our desired map ![]() $\varphi ^*(\mathcal {L}) \rightarrow R^1f_*\mathcal {O}_M$. However, we claim we may derive a compatible sequence from
$\varphi ^*(\mathcal {L}) \rightarrow R^1f_*\mathcal {O}_M$. However, we claim we may derive a compatible sequence from ![]() $\psi _i'$ as follows.
$\psi _i'$ as follows.
Consider the subset in the finite set
consisting of all modulo ![]() $\pi _M$ reductions of
$\pi _M$ reductions of ![]() $\psi _i'$:
$\psi _i'$:
By the pigeonhole principle, there exists a non-trivial map ![]() $\psi _1\in \Sigma _1$ and an infinite subset
$\psi _1\in \Sigma _1$ and an infinite subset ![]() $\mathbb {N}_1\subset \mathbb {N}$ such that
$\mathbb {N}_1\subset \mathbb {N}$ such that ![]() $\psi '_i \ {\rm mod}\ (\pi _M) = \psi _1$ for any
$\psi '_i \ {\rm mod}\ (\pi _M) = \psi _1$ for any ![]() $i\in \mathbb {N}_1$.
$i\in \mathbb {N}_1$.
Suppose we have constructed a compatible sequence ![]() $\psi _1,\psi _2,\ldots,\psi _r$ and an infinite subset
$\psi _1,\psi _2,\ldots,\psi _r$ and an infinite subset ![]() $\mathbb {N}_r\subset \mathbb {N}$ satisfying
$\mathbb {N}_r\subset \mathbb {N}$ satisfying
for any ![]() $i\in \mathbb {N}_r$ and
$i\in \mathbb {N}_r$ and ![]() $j\in \{1,2,\ldots,r\}$. Then we consider the subset in the finite set
$j\in \{1,2,\ldots,r\}$. Then we consider the subset in the finite set
consisting of all modulo ![]() $\pi _M^{r+1}$ reductions
$\pi _M^{r+1}$ reductions ![]() $\psi '_i\ {\rm mod}\ (\pi _M^{r+1})$:
$\psi '_i\ {\rm mod}\ (\pi _M^{r+1})$:
Again by the pigeonhole principle, there exists a non-trivial map ![]() $\psi _{r+1}\in \Sigma _{r+1}$ and an infinite subset
$\psi _{r+1}\in \Sigma _{r+1}$ and an infinite subset ![]() $\mathbb {N}_{r+1}\subset \mathbb {N}_r$ such that
$\mathbb {N}_{r+1}\subset \mathbb {N}_r$ such that ![]() $\psi '_i \ {\rm mod}\ (\pi _M^{r+1}) = \psi _{r+1}$ for any
$\psi '_i \ {\rm mod}\ (\pi _M^{r+1}) = \psi _{r+1}$ for any ![]() $i\in \mathbb {N}_{r+1}$.
$i\in \mathbb {N}_{r+1}$.
Iteratively, we find a sequence ![]() $\psi _1,\psi _2,\ldots$ satisfying
$\psi _1,\psi _2,\ldots$ satisfying
for each ![]() $j>i$. Taking projective limits and tensoring with
$j>i$. Taking projective limits and tensoring with ![]() $M$, one gets a non-zero map
$M$, one gets a non-zero map
Since ![]() $\mathcal {L}\otimes M$ is irreducible,
$\mathcal {L}\otimes M$ is irreducible, ![]() $\psi$ is injective.
$\psi$ is injective.
4. Rigidity
In this section, we prove the following. Recall that ![]() $S=\textrm {Spec}({\mathcal {O}_K[1/N]})$.
$S=\textrm {Spec}({\mathcal {O}_K[1/N]})$.
Lemma 4.1 Let ![]() $\mathcal {H}/S$ be as in § 3. Then, after potentially increasing
$\mathcal {H}/S$ be as in § 3. Then, after potentially increasing ![]() $N$ (equivalently, replacing
$N$ (equivalently, replacing ![]() $S$ by a non-empty Zariski open subset), the relative dimension of
$S$ by a non-empty Zariski open subset), the relative dimension of ![]() $\mathcal {H}/S$ is
$\mathcal {H}/S$ is ![]() $0$.
$0$.
Proof. We have shown that ![]() $\mathcal {H}/S$ is a finite-type Deligne–Mumford stack. To show the desired result, it suffices to show that if
$\mathcal {H}/S$ is a finite-type Deligne–Mumford stack. To show the desired result, it suffices to show that if ![]() $K\hookrightarrow \mathbb {C}$ is an embedding, then
$K\hookrightarrow \mathbb {C}$ is an embedding, then ![]() $\mathcal {H}_{{\mathbb {C}}}$ has dimension
$\mathcal {H}_{{\mathbb {C}}}$ has dimension ![]() $0$. Equivalently, we want to show that if
$0$. Equivalently, we want to show that if ![]() $A_{U_{{\mathbb {C}}}}\rightarrow U_{{\mathbb {C}}}$ is a principally polarized abelian scheme that is totally degenerate at at least one cusp, then it is rigid. This immediately follows from Theorem 8.6 together with Lemma 3.4 and the following text of [Reference SaitoSai93].
$A_{U_{{\mathbb {C}}}}\rightarrow U_{{\mathbb {C}}}$ is a principally polarized abelian scheme that is totally degenerate at at least one cusp, then it is rigid. This immediately follows from Theorem 8.6 together with Lemma 3.4 and the following text of [Reference SaitoSai93].
5. The proof
Proof of Theorem 1.4 First, assume that ![]() ${\mathbb {L}}$ has bad, unipotent reduction around every cusp. Let
${\mathbb {L}}$ has bad, unipotent reduction around every cusp. Let ![]() $\mathcal {T}_1$ be the set of those prime
$\mathcal {T}_1$ be the set of those prime ![]() ${\mathfrak {p}}$ of
${\mathfrak {p}}$ of ![]() $\mathcal {O}_K$ with the following properties: the underlying prime
$\mathcal {O}_K$ with the following properties: the underlying prime ![]() $p$ splits completely in
$p$ splits completely in ![]() $E$, and
$E$, and ![]() $p>\max (N,\ell ^3)$. This is an infinite set by the Cebotarev density theorem. Let
$p>\max (N,\ell ^3)$. This is an infinite set by the Cebotarev density theorem. Let ![]() ${\mathcal {L}}_{{\mathfrak {p}}}$ be the restriction of
${\mathcal {L}}_{{\mathfrak {p}}}$ be the restriction of ![]() ${\mathcal {L}}$ to
${\mathcal {L}}$ to ![]() $U_{{\mathfrak {p}}}$. Then
$U_{{\mathfrak {p}}}$. Then ![]() ${\mathcal {L}}_{{\mathfrak {p}}}$ is irreducible by exactly the same argument as that of the first paragraph of [Reference Snowden and TsimermanST18, Proof of Lemma 24, p. 2053].
${\mathcal {L}}_{{\mathfrak {p}}}$ is irreducible by exactly the same argument as that of the first paragraph of [Reference Snowden and TsimermanST18, Proof of Lemma 24, p. 2053].
There are only finitely may subfields of ![]() $E$. It follows from the pigeonhole principle that there exists a subfield
$E$. It follows from the pigeonhole principle that there exists a subfield ![]() $F\subset E$ such that there exists infinitely many primes
$F\subset E$ such that there exists infinitely many primes ![]() ${\mathfrak {p}}\in \mathcal {T}_1$ such that
${\mathfrak {p}}\in \mathcal {T}_1$ such that ![]() ${\mathcal {L}}_{{\mathfrak {p}}}$ has Frobenius traces in
${\mathcal {L}}_{{\mathfrak {p}}}$ has Frobenius traces in ![]() $F\subset E$. Call the collection of such primes
$F\subset E$. Call the collection of such primes ![]() $\mathcal {T}_2\subset \mathcal {T}_1$. Let
$\mathcal {T}_2\subset \mathcal {T}_1$. Let ![]() $\mathcal {H}$ and
$\mathcal {H}$ and ![]() $\mathcal {H}_{\infty }$ be the moduli spaces from § 3 with
$\mathcal {H}_{\infty }$ be the moduli spaces from § 3 with ![]() $g=8[F:{\mathbb {Q}}]$ and
$g=8[F:{\mathbb {Q}}]$ and ![]() $b=4h\chi _{\text {top}}(U)$. Note that, after increasing
$b=4h\chi _{\text {top}}(U)$. Note that, after increasing ![]() $N$, both spaces have relative dimension
$N$, both spaces have relative dimension ![]() $0$ over
$0$ over ![]() ${\mathcal {O}_K[1/N]}$ by § 4.
${\mathcal {O}_K[1/N]}$ by § 4.
First of all, note that for each ![]() ${\mathfrak {p}}\in \mathcal {T}_2$,
${\mathfrak {p}}\in \mathcal {T}_2$, ![]() $\mathcal {H}_{\infty }(\kappa ({\mathfrak {p}}))\neq \emptyset$. This follows by Lemma 2.7, especially part (3)(iv), together with Lemma 3.6. In more detail: Lemma 2.7 implies that we can find an abelian scheme
$\mathcal {H}_{\infty }(\kappa ({\mathfrak {p}}))\neq \emptyset$. This follows by Lemma 2.7, especially part (3)(iv), together with Lemma 3.6. In more detail: Lemma 2.7 implies that we can find an abelian scheme ![]() $B_{{\mathfrak {U}}_{{\mathfrak {p}}}}\rightarrow {{\mathfrak {U}}_{{\mathfrak {p}}}}$ such that
$B_{{\mathfrak {U}}_{{\mathfrak {p}}}}\rightarrow {{\mathfrak {U}}_{{\mathfrak {p}}}}$ such that ![]() $\mathcal {L}_{{\mathfrak {p}}}^4$ injects in the cohomology, that has semistable reduction at infinity, and such that the Hodge bundle on
$\mathcal {L}_{{\mathfrak {p}}}^4$ injects in the cohomology, that has semistable reduction at infinity, and such that the Hodge bundle on ![]() ${\mathfrak {X}}_{{\mathfrak {p}}}$ has bounded degree. Lemma 3.6 then implies that such an abelian scheme corresponds to a point
${\mathfrak {X}}_{{\mathfrak {p}}}$ has bounded degree. Lemma 3.6 then implies that such an abelian scheme corresponds to a point ![]() $\beta _{{\mathfrak {p}}}$ in
$\beta _{{\mathfrak {p}}}$ in ![]() $\mathcal {H}_{\infty }(\kappa ({\mathfrak {p}}))\subset \mathcal {H}(\kappa ({\mathfrak {p}}))$. Since
$\mathcal {H}_{\infty }(\kappa ({\mathfrak {p}}))\subset \mathcal {H}(\kappa ({\mathfrak {p}}))$. Since ![]() $\mathcal {T}_2$ is infinite and
$\mathcal {T}_2$ is infinite and ![]() $\mathcal {H}_{\infty }/S$ is of finite type, it follows that there exists a finite field extension
$\mathcal {H}_{\infty }/S$ is of finite type, it follows that there exists a finite field extension ![]() $K'/K$ and a point
$K'/K$ and a point ![]() $\beta \in \mathcal {H}(K')$. In fact, as
$\beta \in \mathcal {H}(K')$. In fact, as ![]() $\mathcal {H}_{\infty }$ has relative dimension
$\mathcal {H}_{\infty }$ has relative dimension ![]() $0$, our point
$0$, our point ![]() $\beta$ may be chosen to be compatible with infinitely many of the
$\beta$ may be chosen to be compatible with infinitely many of the ![]() $\beta _{{\mathfrak {p}}}$, where compatibility is defined in the obvious sense. By definition of
$\beta _{{\mathfrak {p}}}$, where compatibility is defined in the obvious sense. By definition of ![]() $\mathcal {H}_\infty$, the point
$\mathcal {H}_\infty$, the point ![]() $\beta \in \mathcal {H}_\infty (K')$ corresponds to an abelian scheme
$\beta \in \mathcal {H}_\infty (K')$ corresponds to an abelian scheme ![]() $B_{U'_{K'}}\rightarrow U'_{K'}$ such that
$B_{U'_{K'}}\rightarrow U'_{K'}$ such that ![]() $\mathcal {L}|_{U'_{K'}}$ injects into the integral
$\mathcal {L}|_{U'_{K'}}$ injects into the integral ![]() $\mathcal {O}_M$ cohomology. By taking a Weil restriction, we obtain an abelian scheme
$\mathcal {O}_M$ cohomology. By taking a Weil restriction, we obtain an abelian scheme ![]() $A_U\rightarrow U$ (of dimension
$A_U\rightarrow U$ (of dimension ![]() $g[K':K]$) such that
$g[K':K]$) such that ![]() ${\mathbb {L}}$ injects into the cohomology of
${\mathbb {L}}$ injects into the cohomology of ![]() $A_U\rightarrow U$. Using Faltings’ semi-simplicity theorem, we conclude that
$A_U\rightarrow U$. Using Faltings’ semi-simplicity theorem, we conclude that ![]() ${\mathbb {L}}$ is, in fact, a summand of the cohomology, as desired.
${\mathbb {L}}$ is, in fact, a summand of the cohomology, as desired.
In general, there exists a finite étale cover ![]() $f\colon U'\rightarrow U$ such that
$f\colon U'\rightarrow U$ such that ![]() $f^*\mathbb {L}$ has the following property. Let
$f^*\mathbb {L}$ has the following property. Let ![]() $C'$ be the compactification of
$C'$ be the compactification of ![]() $U'$, and set
$U'$, and set ![]() $D'$ to be the divisor at infinity. Then for each
$D'$ to be the divisor at infinity. Then for each ![]() $\infty \in D'$, the lisse
$\infty \in D'$, the lisse ![]() $\ell$-adic sheaf
$\ell$-adic sheaf ![]() $f^*\mathbb {L}$ has either good reduction at
$f^*\mathbb {L}$ has either good reduction at ![]() $\infty$ or bad, unipotent reduction at
$\infty$ or bad, unipotent reduction at ![]() $\infty$. There then exists a curve
$\infty$. There then exists a curve ![]() $U'\subset V'\subset C'$, where
$U'\subset V'\subset C'$, where ![]() $f^*\mathbb {L}$ extends to a lisse
$f^*\mathbb {L}$ extends to a lisse ![]() $\ell$-adic sheaf
$\ell$-adic sheaf ![]() $\mathbb {M}'$ on all of
$\mathbb {M}'$ on all of ![]() $V'$ and, moreover, has bad, unipotent reduction around every point in
$V'$ and, moreover, has bad, unipotent reduction around every point in ![]() $C'\setminus V'$. Then the above argument applies, producing an abelian scheme
$C'\setminus V'$. Then the above argument applies, producing an abelian scheme ![]() $A_{V'}\rightarrow V'$ whose cohomology has
$A_{V'}\rightarrow V'$ whose cohomology has ![]() $\mathbb {M}'$ as a summand. Restricting to
$\mathbb {M}'$ as a summand. Restricting to ![]() $U'$ and then applying a Weil restriction of scalars along the finite étale map
$U'$ and then applying a Weil restriction of scalars along the finite étale map ![]() $U'/U$, we obtain the desired result.
$U'/U$, we obtain the desired result.
Acknowledgements
We would like to express our sincere gratitude to the referees for their valuable feedback and constructive criticism, which greatly contributed to the improvement of this paper. R.K. warmly thanks Xia Jie for discussions about his thesis in 2013, Johan de Jong for explaining the importance of the condition ‘generically versally deformed’ for height ![]() $2$, dimension
$2$, dimension ![]() $1$ Barsotti–Tate groups in 2014, and Marco d'Addezio for several enlightening discussions on semistable Barsotti–Tate groups in 2022. K.Z. thanks A. Langer for discussions on elementary transformations of de Rham bundles and A. Javenpeykar for discussions on the degree of automorphic bundles. All three authors would further like to acknowledge the debt of this work to the recent work of Snowden and Tsimerman [Reference Snowden and TsimermanST18]. J.Y. is supported by National Natural Science Foundation of China Grant No. 12201595, the Fundamental Research Funds for the Central Universities and CAS Project for Young Scientists in Basic Research Grant No. YSBR-032. R.K. was partially supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program, grant agreement no. 101020009, project TameHodge. J.Y. and K.Z. are supported by National Natural Science Foundation of China Key Program 12331002.
$1$ Barsotti–Tate groups in 2014, and Marco d'Addezio for several enlightening discussions on semistable Barsotti–Tate groups in 2022. K.Z. thanks A. Langer for discussions on elementary transformations of de Rham bundles and A. Javenpeykar for discussions on the degree of automorphic bundles. All three authors would further like to acknowledge the debt of this work to the recent work of Snowden and Tsimerman [Reference Snowden and TsimermanST18]. J.Y. is supported by National Natural Science Foundation of China Grant No. 12201595, the Fundamental Research Funds for the Central Universities and CAS Project for Young Scientists in Basic Research Grant No. YSBR-032. R.K. was partially supported by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program, grant agreement no. 101020009, project TameHodge. J.Y. and K.Z. are supported by National Natural Science Foundation of China Key Program 12331002.
Conflicts of Interest
None.
Appendix A. Frobenius untwisting and a second proof of Proposition 2.4(2)
In this appendix, we have two goals: we first provide a proof of [Reference XiaXia13, Theorem 6.1] in the context we need, which we use several times, and then we provide a second perspective on the termination of the Frobenius untwisting process in the context of Proposition 2.4.
Before we begin the proofs, we need one preliminary claim. Let ![]() $(\bar {\mathcal {C}}, \mathcal {Z})$ be a lift of
$(\bar {\mathcal {C}}, \mathcal {Z})$ be a lift of ![]() $(\bar {C},Z)$ over
$(\bar {C},Z)$ over ![]() $W(k)$. Let
$W(k)$. Let ![]() $({\mathcal {V}},\nabla )$ be a vector bundle together with a logarithmic connection with nilpotent residues on
$({\mathcal {V}},\nabla )$ be a vector bundle together with a logarithmic connection with nilpotent residues on ![]() $(\bar {\mathcal {C}},\mathcal {Z})/W(k)$, such that
$(\bar {\mathcal {C}},\mathcal {Z})/W(k)$, such that ![]() $\nabla$ is topologically quasi-nilpotent. (Therefore,
$\nabla$ is topologically quasi-nilpotent. (Therefore, ![]() $({\mathcal {V}},\nabla )$ is the value of a logarithmic crystal
$({\mathcal {V}},\nabla )$ is the value of a logarithmic crystal ![]() $(C,Z)$ on the particular thickening
$(C,Z)$ on the particular thickening ![]() $(\bar {\mathcal {C}},\mathcal {Z})$).
$(\bar {\mathcal {C}},\mathcal {Z})$).
Claim A.1 The following two properties hold for ![]() $({\mathcal {V}},\nabla )$.
$({\mathcal {V}},\nabla )$.
(i) The logarithmic isocrystal
 $({\mathcal {V}},\nabla )\otimes \mathbb {Q}_p$ over
$({\mathcal {V}},\nabla )\otimes \mathbb {Q}_p$ over  $(\mathcal {\bar {C}},\mathcal {Z})|_{W(k)[1/p]}$ is semistable and of degree
$(\mathcal {\bar {C}},\mathcal {Z})|_{W(k)[1/p]}$ is semistable and of degree  $0$.
$0$.(ii) The degree of
 ${\mathcal {V}}_p={\mathcal {V}}\otimes \mathbb {F}_p$, the restriction of the vector bundle
${\mathcal {V}}_p={\mathcal {V}}\otimes \mathbb {F}_p$, the restriction of the vector bundle  ${\mathcal {V}}$ to
${\mathcal {V}}$ to  $\bar {C}$, is
$\bar {C}$, is  $0$.
$0$.
Proof of claim To prove that ![]() ${\mathcal {V}}\otimes \mathbb {Q}_p$ has degree
${\mathcal {V}}\otimes \mathbb {Q}_p$ has degree ![]() $0$, it suffices to base change along a map
$0$, it suffices to base change along a map ![]() $W(k)[1/p]\hookrightarrow \mathbb {C}$. Then the result follows from a computation of Esnault and Viehweg [Reference Esnault and ViehwegEV86, Appendix B]. Now semistability follows easily. Indeed, any horizontal subsheaf of
$W(k)[1/p]\hookrightarrow \mathbb {C}$. Then the result follows from a computation of Esnault and Viehweg [Reference Esnault and ViehwegEV86, Appendix B]. Now semistability follows easily. Indeed, any horizontal subsheaf of ![]() ${\mathcal {V}}\otimes \mathbb {Q}_p$ is necessarily a bundle, which is therefore equipped with a logarithmic flat connection and has nilpotent residues. By the first sentence, this implies that this horizontal subsheaf has degree
${\mathcal {V}}\otimes \mathbb {Q}_p$ is necessarily a bundle, which is therefore equipped with a logarithmic flat connection and has nilpotent residues. By the first sentence, this implies that this horizontal subsheaf has degree ![]() $0$, validating semistability.
$0$, validating semistability.
To prove the second statement, it suffices to note that degree, being the first Chern class, is locally constant, see [Reference Krishnamoorthy, Yang and ZuoKYZ20, § 6]; therefore, if the degree of ![]() ${\mathcal {V}}\otimes \mathbb {Q}_p$ is
${\mathcal {V}}\otimes \mathbb {Q}_p$ is ![]() $0$ on
$0$ on ![]() $\bar {\mathcal {C}}$, then so is the degree of
$\bar {\mathcal {C}}$, then so is the degree of ![]() ${\mathcal {V}}_{p}$ on
${\mathcal {V}}_{p}$ on ![]() $\bar {C}$.
$\bar {C}$.
The third term in the following lemma is a special case of [Reference XiaXia13, Theorem 6.1] that we need. In particular, we work in the context of strictly semistable ![]() $p$-divisible groups on
$p$-divisible groups on ![]() $(\bar {C},Z)$, as this allows us to discuss the destabilizing iteration.
$(\bar {C},Z)$, as this allows us to discuss the destabilizing iteration.
Lemma A.2 Let ![]() $G_C\rightarrow C$ be a strictly semistable height
$G_C\rightarrow C$ be a strictly semistable height ![]() $2$, dimension
$2$, dimension ![]() $1$
$1$ ![]() $p$-divisible group on
$p$-divisible group on ![]() $C$. Suppose the Kodaira–Spencer map of
$C$. Suppose the Kodaira–Spencer map of ![]() $G_C\rightarrow C$ is
$G_C\rightarrow C$ is ![]() $0$.
$0$.
(1) Let
 $\mathbb {D}(G_C)$ be the Dieudonné module of
$\mathbb {D}(G_C)$ be the Dieudonné module of  $G_C$. Then the Dieudonné crystal
$G_C$. Then the Dieudonné crystal  $\mathbb {D}(G_C)$ canonically extends to a logarithmic Dieudonné crystal on
$\mathbb {D}(G_C)$ canonically extends to a logarithmic Dieudonné crystal on  $(\bar {C},Z)$.
$(\bar {C},Z)$.(2) Set
 $({\mathcal {M}},\nabla, F,V)$ denote the evaluation of the logarithmic extension of
$({\mathcal {M}},\nabla, F,V)$ denote the evaluation of the logarithmic extension of  $\mathbb {D}(G_C)$ on the log pair
$\mathbb {D}(G_C)$ on the log pair  $(\bar {\mathcal {C}}, \mathcal {Z})$. Then the Hodge line bundle
$(\bar {\mathcal {C}}, \mathcal {Z})$. Then the Hodge line bundle  $L$ in
$L$ in  $\mathcal {M}_p = \mathcal {M}\otimes \mathbb {F}_p$ has positive degree, which is the maximal destabilizing subbundle of
$\mathcal {M}_p = \mathcal {M}\otimes \mathbb {F}_p$ has positive degree, which is the maximal destabilizing subbundle of  $({\mathcal {M}}_p,\nabla _p)$.
$({\mathcal {M}}_p,\nabla _p)$.(3) Then there exists an isogenous
 $p$-divisible group
$p$-divisible group  $G'_C\rightarrow C$, such that the Frobenius pullback
$G'_C\rightarrow C$, such that the Frobenius pullback  $G'_C{}^{(p)}$ is isomorphic to
$G'_C{}^{(p)}$ is isomorphic to  $G_C$.
$G_C$.
Proof. Since ![]() $G_C$ is semistable, the first term follows from [Reference TrihanTri08, Corollary 3.14]. The second term follows from the existence of supersingular points as in Proposition 2.4(1) via the Hasse–Witt map. Consider the Kodaira–Spencer map
$G_C$ is semistable, the first term follows from [Reference TrihanTri08, Corollary 3.14]. The second term follows from the existence of supersingular points as in Proposition 2.4(1) via the Hasse–Witt map. Consider the Kodaira–Spencer map
By assumption ![]() $\theta =0$, thus
$\theta =0$, thus ![]() $L\subset ({\mathcal {M}}_p,\nabla _p)$ is a horizontal subbundle. Since
$L\subset ({\mathcal {M}}_p,\nabla _p)$ is a horizontal subbundle. Since ![]() $\deg {\mathcal {M}}_p=0$ and
$\deg {\mathcal {M}}_p=0$ and ![]() $\deg L>0$, the line bundle
$\deg L>0$, the line bundle ![]() $L$ is just the maximal destabilizing subbundle of
$L$ is just the maximal destabilizing subbundle of ![]() $({\mathcal {M}}_p,\nabla _p)$.
$({\mathcal {M}}_p,\nabla _p)$.
For the third term, We mainly follows Xia's original proof. Set ![]() $({\mathcal {M}}',\nabla ')$ to be the kernel of the following composition map
$({\mathcal {M}}',\nabla ')$ to be the kernel of the following composition map
where ![]() $\pi \colon ({\mathcal {M}},\nabla )\rightarrow ({\mathcal {M}}_p,\nabla _p)$ is the reduction modulo
$\pi \colon ({\mathcal {M}},\nabla )\rightarrow ({\mathcal {M}}_p,\nabla _p)$ is the reduction modulo ![]() $p$ map. In particular, one has
$p$ map. In particular, one has
The crucial point is to show the Frobenius structure and the Verschiebung extend; if we show this, then we will obtain a new logarithmic Dieudonné module ![]() $({\mathcal {M}}',\nabla ',F',V').$
$({\mathcal {M}}',\nabla ',F',V').$
Locally, over an affine open subset ![]() $\mathcal {U}=\mathrm {Spec}(R)$, we choose a lifting
$\mathcal {U}=\mathrm {Spec}(R)$, we choose a lifting ![]() $\Phi \colon \widehat {R}\rightarrow \widehat {R}$ of the absolute Frobenius map
$\Phi \colon \widehat {R}\rightarrow \widehat {R}$ of the absolute Frobenius map ![]() $\sigma \colon R/pR\rightarrow R/pR$. Then the Frobenius structure and Verschiebung structure are given by
$\sigma \colon R/pR\rightarrow R/pR$. Then the Frobenius structure and Verschiebung structure are given by
Recall [Reference de JongdJ95, Proposition 2.5.2], ![]() $L$ is the unique subbundle of
$L$ is the unique subbundle of ![]() ${\mathcal {M}}_p$ such that
${\mathcal {M}}_p$ such that
In particular,
This implies that
and that the Frobenius structure ![]() $F$ can be restricted onto
$F$ can be restricted onto ![]() $({\mathcal {M}}',\nabla ')$, denoted by
$({\mathcal {M}}',\nabla ')$, denoted by ![]() $F'$. Similarly,
$F'$. Similarly,
This implies that
and that the Verschiebung structure ![]() $V$ can be restricted onto
$V$ can be restricted onto ![]() $({\mathcal {M}}',\nabla ')$, denoted by
$({\mathcal {M}}',\nabla ')$, denoted by ![]() $V'$. The module
$V'$. The module ![]() $({\mathcal {M}}, \nabla, F, V)'$ is the realization of the
$({\mathcal {M}}, \nabla, F, V)'$ is the realization of the ![]() $\mathbb {D}(G'_C)$ of a
$\mathbb {D}(G'_C)$ of a ![]() $p$-divisible group
$p$-divisible group ![]() $G'_C$ which satisfies
$G'_C$ which satisfies ![]() $G'_C{}^{(p)}=G$ by de Jong's fundamental theorem.
$G'_C{}^{(p)}=G$ by de Jong's fundamental theorem.
Second proof of Proposition 2.4(2) Recall that a ![]() $p$-divisible group is called generically versally deformed if the corresponding Kodaira–Spencer map is non-zero. From the third term in Lemma A.2, one may construct inductively:
$p$-divisible group is called generically versally deformed if the corresponding Kodaira–Spencer map is non-zero. From the third term in Lemma A.2, one may construct inductively:
(1) an infinite sequence of
 $p$-divisible groups over
$p$-divisible groups over  $C$
such that
$C$
such that \[ G^0_C=G_C,G^1_C,G^2_C,\ldots \]
\[ G^0_C=G_C,G^1_C,G^2_C,\ldots \]
 $(G^{i+1}_{C})^{(p)}=G^i_C$ for all
$(G^{i+1}_{C})^{(p)}=G^i_C$ for all  $i\geq 0$ and whose Kodaira–Spencer maps are all zero; or
$i\geq 0$ and whose Kodaira–Spencer maps are all zero; or(2) a finite sequence of
 $p$-divisible groups
such that
$p$-divisible groups
such that \[ G^0_C=G_C,G^1_C,\ldots, G^r_C \]
\[ G^0_C=G_C,G^1_C,\ldots, G^r_C \]
 $(G^{i+1}_{C})^{(p)}=G^i_C$, the Kodaira–Spencer maps of
$(G^{i+1}_{C})^{(p)}=G^i_C$, the Kodaira–Spencer maps of  $G^i_C$ are zero for all
$G^i_C$ are zero for all  ${i\in \{0,\ldots,r-1\}}$, and the Kodaira–Spencer map of
${i\in \{0,\ldots,r-1\}}$, and the Kodaira–Spencer map of  $G^{r}_C$ is non-zero.
$G^{r}_C$ is non-zero.
To prove the second term of Proposition 2.4, one only need to show that the first case does not appear. Suppose we are in the first case. By a method of Langer in [Reference LangerLan14, Theorem 5.1], we will construct a contradiction.
Let ![]() $({\mathcal {M}}^i,\nabla ^i,F^i,V^i)$ be the logarithmic Dieudonné module associated to
$({\mathcal {M}}^i,\nabla ^i,F^i,V^i)$ be the logarithmic Dieudonné module associated to ![]() $G^i_C$ and let
$G^i_C$ and let ![]() $L^i$ be the Hodge line bundle in
$L^i$ be the Hodge line bundle in ![]() ${\mathcal {M}}_p^i$. According the construction of
${\mathcal {M}}_p^i$. According the construction of ![]() $G^i_C$ as in the proof of Lemma A.2, one has
$G^i_C$ as in the proof of Lemma A.2, one has
where ![]() $({\mathcal {M}}^{i+1},\nabla ^{i+1})$ to be the kernel of the following composition map
$({\mathcal {M}}^{i+1},\nabla ^{i+1})$ to be the kernel of the following composition map
where ![]() $\pi \colon ({\mathcal {M}}^i,\nabla ^i)\rightarrow ({\mathcal {M}}^i_p,\nabla ^i_p)$ is the reduction modulo
$\pi \colon ({\mathcal {M}}^i,\nabla ^i)\rightarrow ({\mathcal {M}}^i_p,\nabla ^i_p)$ is the reduction modulo ![]() $p$ map. In particular, one has
$p$ map. In particular, one has
Denote
In the following, we show that the generic fiber ![]() $\overline {{\mathcal {M}}}^m \otimes K$ of
$\overline {{\mathcal {M}}}^m \otimes K$ of ![]() $\overline {{\mathcal {M}}}^m$ is a destabilizing quotient of
$\overline {{\mathcal {M}}}^m$ is a destabilizing quotient of ![]() ${\mathcal {M}}^m\otimes K = {\mathcal {M}}_K$ for sufficiently large
${\mathcal {M}}^m\otimes K = {\mathcal {M}}_K$ for sufficiently large ![]() $m\gg 0$; this will contradict semistability of
$m\gg 0$; this will contradict semistability of ![]() ${\mathcal {M}}_K$.
${\mathcal {M}}_K$.
From (A.4) and the construction of the sequence, one has exact sequences of ![]() $\mathcal {O}_{{\mathfrak {X}}_{\mathfrak {p}}}$-modules
$\mathcal {O}_{{\mathfrak {X}}_{\mathfrak {p}}}$-modules
and
Denote by ![]() $C^n$ the kernel of the composition
$C^n$ the kernel of the composition ![]() $L^{n+1} \rightarrow M_p^{n+1} \rightarrow L^n$. By the same reason as in the proof of [Reference LangerLan14, Theorem 5.1],
$L^{n+1} \rightarrow M_p^{n+1} \rightarrow L^n$. By the same reason as in the proof of [Reference LangerLan14, Theorem 5.1], ![]() $C^n=0$ for sufficient large
$C^n=0$ for sufficient large ![]() $n$. By eliminating the first finitely many terms, we may assume
$n$. By eliminating the first finitely many terms, we may assume ![]() $C^n=0$ for all
$C^n=0$ for all ![]() $n\geq 0$. Thus, one gets injections
$n\geq 0$. Thus, one gets injections
Since the slope of ![]() $L^n$ is non-increasing and also non-negative, the sequence
$L^n$ is non-increasing and also non-negative, the sequence ![]() $L^n$ stabilizes to some
$L^n$ stabilizes to some ![]() $L$. Since
$L$. Since ![]() $\deg L^n + \deg N^n = \deg {\mathcal {M}}^n_{\mathfrak {p}} = 0$, the sequence
$\deg L^n + \deg N^n = \deg {\mathcal {M}}^n_{\mathfrak {p}} = 0$, the sequence ![]() $N^n$ stabilizes to some
$N^n$ stabilizes to some ![]() $N$. Once again, by eliminating the first finitely many terms, we may assume
$N$. Once again, by eliminating the first finitely many terms, we may assume ![]() $L^n = L$ and
$L^n = L$ and ![]() $N^n=N$ for all
$N^n=N$ for all ![]() $n\geq 0$. In particular, the composition map
$n\geq 0$. In particular, the composition map
is an isomorphism for all ![]() $n\geq 0$. Thus,
$n\geq 0$. Thus,
and
for each ![]() $n\geq 0$. We show that
$n\geq 0$. We show that ![]() ${\mathcal {M}}^i=p^{i}{\mathcal {M}}^0 + {\mathcal {M}}^n$ for any
${\mathcal {M}}^i=p^{i}{\mathcal {M}}^0 + {\mathcal {M}}^n$ for any ![]() $0\leq i\leq n$ and
$0\leq i\leq n$ and ![]() $p {\mathcal {M}}^{n-1} = p {\mathcal {M}}^0 \cap {\mathcal {M}}^n$ as follows:
$p {\mathcal {M}}^{n-1} = p {\mathcal {M}}^0 \cap {\mathcal {M}}^n$ as follows:
 \begin{align} {\mathcal{M}}^i &
\overset{(A.5)}{=} p{\mathcal{M}}^{i-1}
+{\mathcal{M}}^{i+1} \overset{(A.5)}{=}
p{\mathcal{M}}^{i-1} + p{\mathcal{M}}^{i+1} +
{\mathcal{M}}^{i+2} \nonumber\\ &
\overset{(A.5)}{=}p{\mathcal{M}}^{i-1} +
p{\mathcal{M}}^{i+1} + \cdots + p{\mathcal{M}}^{n-1} +
{\mathcal{M}}^n = p{\mathcal{M}}^{i-1} + {\mathcal{M}}^n,
\end{align}
\begin{align} {\mathcal{M}}^i &
\overset{(A.5)}{=} p{\mathcal{M}}^{i-1}
+{\mathcal{M}}^{i+1} \overset{(A.5)}{=}
p{\mathcal{M}}^{i-1} + p{\mathcal{M}}^{i+1} +
{\mathcal{M}}^{i+2} \nonumber\\ &
\overset{(A.5)}{=}p{\mathcal{M}}^{i-1} +
p{\mathcal{M}}^{i+1} + \cdots + p{\mathcal{M}}^{n-1} +
{\mathcal{M}}^n = p{\mathcal{M}}^{i-1} + {\mathcal{M}}^n,
\end{align} \begin{align} {\mathcal{M}}^i &
\overset{(A.7)}{=} p{\mathcal{M}}^{i-1} +
{\mathcal{M}}^n = \underbrace{p(p(\cdots
p(p}_i{\mathcal{M}}^0+{\mathcal{M}}^n)+
{\mathcal{M}}^n)\cdots + {\mathcal{M}}^n) +
{\mathcal{M}}^n\nonumber\\ & \ \, = p^i{\mathcal{M}}^0 +
{\mathcal{M}}^n,
\end{align}
\begin{align} {\mathcal{M}}^i &
\overset{(A.7)}{=} p{\mathcal{M}}^{i-1} +
{\mathcal{M}}^n = \underbrace{p(p(\cdots
p(p}_i{\mathcal{M}}^0+{\mathcal{M}}^n)+
{\mathcal{M}}^n)\cdots + {\mathcal{M}}^n) +
{\mathcal{M}}^n\nonumber\\ & \ \, = p^i{\mathcal{M}}^0 +
{\mathcal{M}}^n,
\end{align}and
 \begin{align} p{\mathcal{M}}^{n-1} &
\overset{(A.6)}{=} p{\mathcal{M}}^{n-2} \cap
{\mathcal{M}}^n \overset{(A.6)}{=}
(p{\mathcal{M}}^{n-3} \cap {\mathcal{M}}_{n-1} )\cap
{\mathcal{M}}^n \nonumber\\ & \overset{(A.6)}{=}
((\cdots(p{\mathcal{M}}^{0}\cap {\mathcal{M}}_1)\cap
\cdots) \cap {\mathcal{M}}_{n-1} )\cap {\mathcal{M}}^n =
p{\mathcal{M}}^0\cap {\mathcal{M}}^n.
\end{align}
\begin{align} p{\mathcal{M}}^{n-1} &
\overset{(A.6)}{=} p{\mathcal{M}}^{n-2} \cap
{\mathcal{M}}^n \overset{(A.6)}{=}
(p{\mathcal{M}}^{n-3} \cap {\mathcal{M}}_{n-1} )\cap
{\mathcal{M}}^n \nonumber\\ & \overset{(A.6)}{=}
((\cdots(p{\mathcal{M}}^{0}\cap {\mathcal{M}}_1)\cap
\cdots) \cap {\mathcal{M}}_{n-1} )\cap {\mathcal{M}}^n =
p{\mathcal{M}}^0\cap {\mathcal{M}}^n.
\end{align}
In particular, there is an ![]() $W_n=W(k)/p^n$ module structure on
$W_n=W(k)/p^n$ module structure on ![]() ${\mathcal {M}}^0/{\mathcal {M}}^n$. Consider
${\mathcal {M}}^0/{\mathcal {M}}^n$. Consider
 \begin{align*} ({\mathcal{M}}^0/{\mathcal{M}}^n)\otimes_{W_n} (pW_n/p^nW_n) & \cong ({\mathcal{M}}^0/{\mathcal{M}}^n)\otimes_{W_n} W_n/p^{n-1}\\ & = {\mathcal{M}}^0/(p^{n-1} {\mathcal{M}}^0+{\mathcal{M}}^n) = {\mathcal{M}}^0/{\mathcal{M}}^{n-1} \\ & \cong p {\mathcal{M}}^0/ p {\mathcal{M}}^{n-1} = p {\mathcal{M}}^0/ (p {\mathcal{M}}^0 \cap {\mathcal{M}}^n)\\ & \cong (p {\mathcal{M}}^0+{\mathcal{M}}^n)/{\mathcal{M}}^n = {\mathcal{M}}^1/{\mathcal{M}}^n, \end{align*}
\begin{align*} ({\mathcal{M}}^0/{\mathcal{M}}^n)\otimes_{W_n} (pW_n/p^nW_n) & \cong ({\mathcal{M}}^0/{\mathcal{M}}^n)\otimes_{W_n} W_n/p^{n-1}\\ & = {\mathcal{M}}^0/(p^{n-1} {\mathcal{M}}^0+{\mathcal{M}}^n) = {\mathcal{M}}^0/{\mathcal{M}}^{n-1} \\ & \cong p {\mathcal{M}}^0/ p {\mathcal{M}}^{n-1} = p {\mathcal{M}}^0/ (p {\mathcal{M}}^0 \cap {\mathcal{M}}^n)\\ & \cong (p {\mathcal{M}}^0+{\mathcal{M}}^n)/{\mathcal{M}}^n = {\mathcal{M}}^1/{\mathcal{M}}^n, \end{align*}
where the map can be easily checked to be given by ![]() $\overline {m} \otimes \overline {a} \mapsto \overline {am}$ for any
$\overline {m} \otimes \overline {a} \mapsto \overline {am}$ for any ![]() $m\in {\mathcal {M}}^0$ and any
$m\in {\mathcal {M}}^0$ and any ![]() $a\in p$. One also has
$a\in p$. One also has
which implies the following sequence is exact
Thus, ![]() $\mathrm {Tor}^{W/p^n}(k,{\mathcal {M}}^0/{\mathcal {M}}^n)=0$ and
$\mathrm {Tor}^{W/p^n}(k,{\mathcal {M}}^0/{\mathcal {M}}^n)=0$ and ![]() ${\mathcal {M}}^0/{\mathcal {M}}^n$ is flat over
${\mathcal {M}}^0/{\mathcal {M}}^n$ is flat over ![]() $W_n$. It follows that
$W_n$. It follows that ![]() $\widetilde {{\mathcal {M}}}^0 = \varprojlim _{n\geq 0} {\mathcal {M}}^0/{\mathcal {M}}^n$ is a
$\widetilde {{\mathcal {M}}}^0 = \varprojlim _{n\geq 0} {\mathcal {M}}^0/{\mathcal {M}}^n$ is a ![]() $W(k)$-flat coherent
$W(k)$-flat coherent ![]() $\mathcal {O}_{\bar {\mathcal {C}}}$-module having a filtration with quotients isomorphic to
$\mathcal {O}_{\bar {\mathcal {C}}}$-module having a filtration with quotients isomorphic to ![]() $N$. Thus,
$N$. Thus, ![]() $\widetilde {{\mathcal {M}}}^0\otimes W(k)[1/p]$ is a destabilizing quotient of
$\widetilde {{\mathcal {M}}}^0\otimes W(k)[1/p]$ is a destabilizing quotient of ![]() ${\mathcal {M}}^0\otimes W(k)[1/p],$ which contradicts the semistability of
${\mathcal {M}}^0\otimes W(k)[1/p],$ which contradicts the semistability of ![]() ${\mathcal {M}}^0\otimes W(k)[1/p].$
${\mathcal {M}}^0\otimes W(k)[1/p].$