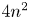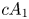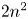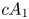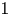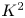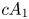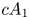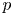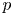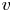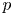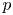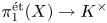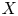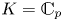Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
2 n2-inequality for cA1 points and applications to birational rigidity
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1551-1595
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BPS invariants from p-adic integrals
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1525-1550
-
- Article
-
- You have access
- HTML
- Export citation
Thin links and Conway spheres
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1467-1524
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A geometric p-adic Simpson correspondence in rank one
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1433-1466
-
- Article
- Export citation