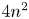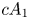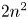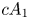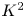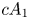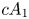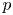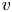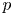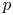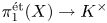Volume 160 - Issue 7 - July 2024
Research Article
2 n2-inequality for cA1 points and applications to birational rigidity
- Part of:
-
- Published online by Cambridge University Press:
- 29 May 2024, pp. 1551-1595
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BPS invariants from p-adic integrals
- Part of:
-
- Published online by Cambridge University Press:
- 30 May 2024, pp. 1525-1550
-
- Article
-
- You have access
- HTML
- Export citation
Thin links and Conway spheres
- Part of:
-
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1467-1524
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A geometric p-adic Simpson correspondence in rank one
- Part of:
-
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1433-1466
-
- Article
- Export citation