Hostname: page-component-84b7d79bbc-5lx2p Total loading time: 0 Render date: 2024-07-26T13:50:36.288Z Has data issue: false hasContentIssue false
  • English
  • Français

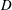$D$-modules on spaces of rational maps

Part of: Families, fibrations

Published online by Cambridge University Press:  31 March 2014

Jonathan Barlev
Jonathan Barlev*
Affiliation:
Department of Mathematics, University of Chicago, 5734 University Avenue, Chicago, IL 60637, USA email jonathan.barlev@math.uchicago.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 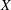$X$ be an algebraic curve. We study the problem of parametrizing geometric structures over 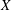$X$ which are only generically defined. For example, parametrizing generically defined maps (rational maps) from 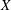$X$ to a fixed target scheme 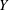$Y$. There are three methods for constructing functors of points for such moduli problems (all originally due to Drinfeld), and we show that the resulting functors are equivalent in the fppf Grothendieck topology. As an application, we obtain three presentations for the category of 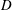$D$-modules ‘on’ 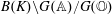$B(K)\backslash G(\mathbb{A})/G(\mathbb{O})$, and we combine results about this category coming from the different presentations.

Keywords

D-modulesrational mapcontractibilitygeometric Langlands

MSC classification

Secondary: 14D24: Geometric Langlands program
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 5 , May 2014 , pp. 835 - 876
Copyright
© The Author 2014 

References

Beilinson, A. and Drinfeld, V., Chiral algebras, American Mathematical Society Colloquium Publications, vol. 51 (American Mathematical Society, Providence, RI, 2004); MR 2058353 (2005d:17007).Google Scholar
Braverman, A., Finkelberg, M., Gaitsgory, D. and Mirković, I., Intersection cohomology of Drinfeld’s compactifications, Selecta Math. (N.S.) 8 (2002), 381–418; MR 1931170 (2003h:14060).Google Scholar
Braverman, A. and Gaitsgory, D., Geometric Eisenstein series, Invent. Math. 150 (2002), 287–384; MR 1933587 (2003k:11109).Google Scholar
Drinfel’d, V. G. and Simpson, Carlos, B-structures on G-bundles and local triviality, Math. Res. Lett. 2 (1995), 823–829; MR 1362973 (96k:14013).Google Scholar
Finkelberg, M. and Mirković, I., Semi-infinite flags. I. Case of global curve P1, in Differential topology, infinite-dimensional Lie algebras, and applications, American Mathematical Society Translations, Series 2, vol. 194 (American Mathematical Society, Providence, RI, 1999), 81–112; MR 1729360 (2001j:14029).Google Scholar
Gaitsgory, D., The extended Whittaker category, Preprint (2010), http://math.harvard.edu/∼gaitsgde/GL/extWhit.pdf.Google Scholar
Gaitsgory, D., Notes on geometric Langlands: generalities on DG categories, Preprint (2011), http://math.harvard.edu/∼gaitsgde/GL/textDG.pdf.Google Scholar
Gaitsgory, D., Contractibility of the space of rational maps, Invent. Math. 191 (2013), 91–196; MR 3004779.CrossRefGoogle Scholar
Gaitsgory, D. and Rozenblyum, N., Crystals and d-modules, Preprint (2011), http://math.harvard.edu/∼gaitsgde/GL/IndCohtext.pdf.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977); MR 0463157 (57 #3116).CrossRefGoogle Scholar
Johnstone, P. T., Sketches of an elephant: a topos theory compendium. Vol. 2, Oxford Logic Guides, vol. 44 (Clarendon Press, Oxford, 2002); MR 2063092 (2005g:18007).Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009); MR 2522659 (2010j:18001).CrossRefGoogle Scholar
Lurie, J., Higher algebra, Preprint (2011), http://math.harvard.edu/∼lurie/papers/higheralgebra.pdf.Google Scholar
Lurie, J., Structured spaces, Preprint (2011), http://math.harvard.edu/∼lurie/papers/DAG-V.pdf.Google Scholar