Hostname: page-component-848d4c4894-89wxm Total loading time: 0 Render date: 2024-07-05T10:55:04.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramification theory and perfectoid spaces

Part of: Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  03 April 2014

Shin Hattori
Shin Hattori*
Affiliation:
Faculty of Mathematics, Kyushu University, 744 Motooka, Nishi-ku, Fukuoka, 819-0395, Japan email shin-h@math.kyushu-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 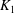$K_1$ and 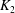$K_2$ be complete discrete valuation fields of residue characteristic 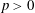$p>0$. Let 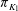$\pi _{K_1}$ and 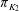$\pi _{K_2}$ be their uniformizers. Let 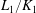$L_1/K_1$ and 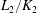$L_2/K_2$ be finite extensions with compatible isomorphisms of rings 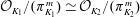$\mathcal{O}_{K_1}/(\pi _{K_1}^m)\, {\simeq }\, \mathcal{O}_{K_2}/(\pi _{K_2}^m)$ and 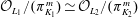$\mathcal{O}_{L_1}/(\pi _{K_1}^m)\, {\simeq }\, \mathcal{O}_{L_2}/(\pi _{K_2}^m)$ for some positive integer 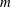$m$ which is no more than the absolute ramification indices of 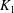$K_1$ and 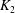$K_2$. Let 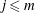$j\leq m$ be a positive rational number. In this paper, we prove that the ramification of 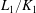$L_1/K_1$ is bounded by 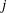$j$ if and only if the ramification of 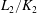$L_2/K_2$ is bounded by 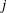$j$. As an application, we prove that the categories of finite separable extensions of 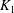$K_1$ and 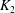$K_2$ whose ramifications are bounded by 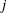$j$ are equivalent to each other, which generalizes a theorem of Deligne to the case of imperfect residue fields. We also show the compatibility of Scholl’s theory of higher fields of norms with the ramification theory of Abbes–Saito, and the integrality of small Artin and Swan conductors of 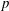$p$-adic representations with finite local monodromy.

Keywords

ramificationtruncated discrete valuation ringsperfectoid spaces

MSC classification

Secondary: 11S15: Ramification and extension theory
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 5 , May 2014 , pp. 798 - 834
Copyright
© The Author 2014 

References

Abbes, A. and Saito, T., Ramification of local fields with imperfect residue fields I, Amer. J. Math. 124 (2002), 879–920.Google Scholar
Abbes, A. and Saito, T., Ramification of local fields with imperfect residue fields II, Kazuya Kato’s fiftieth birthday, Doc. Math Extra Vol. (2003), 5–72.Google Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis. A systematic approach to rigid analytic geometry, Grundlehren der Mathematischen Wissenschaften, vol. 261 (Springer, Berlin, 1984).Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Formal and rigid geometry IV. The reduced fibre theorem, Invent. Math. 119 (1995), 361–398.Google Scholar
Deligne, P., Les corps locaux de caractéristique p, limites de corps locaux de caractéristique 0, in Representations of reductive groups over a local field (Travaux en Cours, Hermann, Paris, 1984), 119–157.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique IV. Étude locale des schémas et des morphismes de schémas I, Publ. Math. Inst. Hautes Études Sci. 20 (1964).CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique IV. Étude locale des schémas et des morphismes de schémas IV, Publ. Math. Inst. Hautes Études Sci. 32 (1967).Google Scholar
Hattori, S., Ramification of a finite flat group scheme over a local field, J. Number Theory 118 (2006), 145–154.Google Scholar
Hattori, S., Ramification correspondence of finite flat group schemes over equal and mixed characteristic local fields, J. Number Theory 132 (2012), 2084–2102.CrossRefGoogle Scholar
Hattori, S., On lower ramification subgroups and canonical subgroups, Algebra Number Theory, to appear, arXiv:1208.5326v2.Google Scholar
Hiranouchi, T. and Taguchi, Y., Extensions of truncated discrete valuation rings, Pure Appl. Math. Q. 4 (2008), 1205–1214.CrossRefGoogle Scholar
Huber, R., Continuous valuations, Math. Z. 212 (1993), 455–477.Google Scholar
Huber, R., A generalization of formal schemes and rigid analytic varieties, Math. Z. 217 (1994), 513–551.CrossRefGoogle Scholar
Huber, R., Étale cohomology of rigid analytic varieties and adic spaces, Aspects of Mathematics, vol. E30 (Vieweg, Braunschweig, 1996).Google Scholar
Ohkubo, S., On differential modules associated to de Rham representations in the imperfect residue field case, Preprint (2013), arXiv:1307.8110v2.Google Scholar
Scholl, A. J., Higher fields of norms and (ϕ,Γ)-modules, Doc. Math Extra Vol. (2006), 685–709.Google Scholar
Scholze, P., Perfectoid spaces, Publ. Math. Inst. Hautes Études Sci. 116 (2012), 245–313.Google Scholar
Serre, J.-P., Corps Locaux, Publications de l’Université de Nancago, No. VIII. (Hermann, Paris, 1968).Google Scholar
Wintenberger, J.-P., Le corps des normes de certaines extensions infinies de corps locaux; applications, Ann. Sci. Éc. Norm. Supér. (4) 16 (1983), 59–89.Google Scholar
Xiao, L., On ramification filtrations and p-adic differential modules I: the equal characteristic case, Algebra Number Theory 4 (2010), 969–1027.Google Scholar
Xiao, L., On ramification filtrations and p-adic differential equations II: mixed characteristic case, Compositio Math. 148 (2012), 415–463.Google Scholar