Research Article
A theory of polytopes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 1-24
-
- Article
-
- You have access
- Export citation
A note on strong Ditkin algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 25-30
-
- Article
-
- You have access
- Export citation
Positive definite functions and relative property (T) for subgroups of discrete groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 31-39
-
- Article
-
- You have access
- Export citation
On group uniformities on square of a space and extending pseudometrics II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 41-61
-
- Article
-
- You have access
- Export citation
CSA-groups and separated free constructions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 63-84
-
- Article
-
- You have access
- Export citation
Sets of differentials and smoothness of convex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 91-96
-
- Article
-
- You have access
- Export citation
Rank one Drinfeld modules on hyperelliptic curves
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 85-90
-
- Article
-
- You have access
- Export citation
Smooth families of fibrations and analytic selections of polynomial hulls
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 97-105
-
- Article
-
- You have access
- Export citation
Groups 2-Transitive on a set of their Sylow subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 117-136
-
- Article
-
- You have access
- Export citation
Rings characterised by semiprimitive modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 107-116
-
- Article
-
- You have access
- Export citation
On the maximal circumradius of a planar convex set containing one lattice point
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-151
-
- Article
-
- You have access
- Export citation
On loops which have dihedral 2-groups as inner mapping groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 153-160
-
- Article
-
- You have access
- Export citation
Separable determination of Fréchet differentiability of convex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-167
-
- Article
-
- You have access
- Export citation
Maximum principles for a class of semilinear elliptic boundary-value problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-175
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 52 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 52 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 or the product uniformity u
or the product uniformity u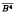 such that there is no analytic selection of the polynomial hull of Σ
such that there is no analytic selection of the polynomial hull of Σ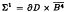 . In particular these examples show that the continuity method for describing the polynomial hull of a fibration over ∂
. In particular these examples show that the continuity method for describing the polynomial hull of a fibration over ∂