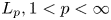37 results in 34Lxx
Time almost periodicity for solutions of Toda lattice equation with almost periodic initial datum
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-40
-
- Article
- Export citation
Spectral identities for Schrödinger operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal inverse problems of potentials for two given eigenvalues of Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 March 2024, pp. 1-24
-
- Article
-
- You have access
- HTML
- Export citation
The lower bounds of non-real eigenvalues for singular indefinite Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1-10
-
- Article
- Export citation
The Lp convergence of Fourier series on triangular domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 453-474
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singular boundary conditions for Sturm–Liouville operators via perturbation theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 23 June 2022, pp. 1110-1146
- Print publication:
- August 2023
-
- Article
- Export citation
On the spectrum of non-self-adjoint Dirac operators with quasi-periodic boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 26 May 2022, pp. 1099-1117
- Print publication:
- August 2023
-
- Article
- Export citation
Jump phenomena of the n-th eigenvalue of discrete Sturm–Liouville problems with application to the continuous case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 02 March 2022, pp. 619-653
- Print publication:
- April 2023
-
- Article
- Export citation
Spectral properties of a beam equation with eigenvalue parameter occurring linearly in the boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 30 July 2021, pp. 780-801
- Print publication:
- June 2022
-
- Article
- Export citation
Markov chain approximation of one-dimensional sticky diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2021, pp. 335-369
- Print publication:
- June 2021
-
- Article
- Export citation
A characterization of singular Schrödinger operators on the half-line
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 923-941
- Print publication:
- December 2021
-
- Article
- Export citation
Estimates for sums and gaps of eigenvalues of Laplacians on measure spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 842-861
- Print publication:
- April 2021
-
- Article
- Export citation
Generalizations of Menchov–Rademacher Theorem and Existence of Wave Operators in Schrödinger Evolution
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 20 December 2019, pp. 360-382
- Print publication:
- April 2021
-
- Article
- Export citation
A priori bounds and existence of non-real eigenvalues for singular indefinite Sturm–Liouville problems with limit-circle type endpoints
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 07 June 2019, pp. 2607-2619
- Print publication:
- October 2020
-
- Article
- Export citation
Spectral partitions for Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 22 May 2019, pp. 2155-2173
- Print publication:
- August 2020
-
- Article
- Export citation
A tale of two approaches to heteroclinic solutions for Φ-Laplacian systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 14 May 2019, pp. 2535-2572
- Print publication:
- October 2020
-
- Article
- Export citation
Spectra of a class of non-symmetric operators in Hilbert spaces with applications to singular differential operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 February 2019, pp. 1769-1790
- Print publication:
- August 2020
-
- Article
- Export citation
Estimates for the order of Nevanlinna matrices and a Berezanskii-type theorem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 1637-1661
- Print publication:
- December 2019
-
- Article
- Export citation
Chaotic backward shift operator on Chebyshev polynomials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 1025-1037
-
- Article
- Export citation
MULTIPLICITIES OF EIGENVALUES OF THE DIFFUSION OPERATOR WITH RANDOM JUMPS FROM THE BOUNDARY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 101-113
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation