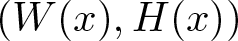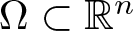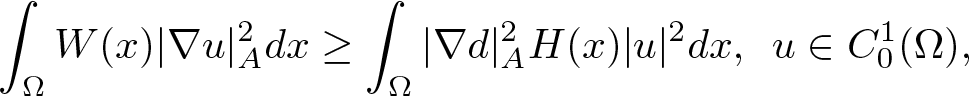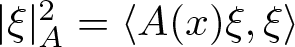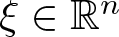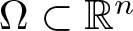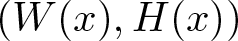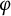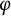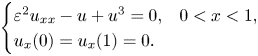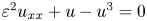91 results in 34Axx
ANALYSIS OF A DISCRETIZED FRACTIONAL-ORDER PREY–PREDATOR MODEL UNDER WIND EFFECT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 02 April 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hardy and Rellich Inequalities with Bessel Pairs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 March 2025, pp. 1-18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal inventory control with state-dependent jumps
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-32
-
- Article
- Export citation
Spectral identities for Schrödinger operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 January 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uniqueness theorems for meromorphic inner functions and canonical systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 124-140
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Flocking dynamics of agents moving with a constant speed and a randomly switching topology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 30 April 2024, pp. 419-447
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DETECTING MOISTURE IN BAUXITE USING MICROWAVES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 4 / October 2023
- Published online by Cambridge University Press:
- 17 April 2024, pp. 308-346
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theoretical study of a
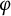 $\varphi $-Hilfer fractional differential system in Banach spaces
$\varphi $-Hilfer fractional differential system in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 27 February 2024, pp. 742-759
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Absolute concentration robustness and multistationarity in reaction networks: Conditions for coexistence
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 02 January 2024, pp. 566-600
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Trend to equilibrium solution for the discrete Safronov–Dubovskiĭ aggregation equation with forcing
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 November 2023, pp. 1-24
-
- Article
- Export citation
Asymptotic formulas of the eigenvalues for the linearization of the scalar field equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A nonconservative kinetic framework under the action of an external force field: Theoretical results with application inspired to ecology
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 1170-1186
-
- Article
- Export citation
Rotating periodic solutions for p-Laplacian differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 1604-1633
- Print publication:
- October 2024
-
- Article
-
- You have access
- HTML
- Export citation
Interface behaviour of the slow diffusion equation with strong absorption: Intermediate-asymptotic properties
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1099-1132
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spreading dynamics of a discrete Nicholson's blowflies equation with distributed delay
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 746-768
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
Positive solutions to the prey–predator equations with dormancy of predators
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 96-108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radial solvability for Pucci-Lane-Emden systems in annuli
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 March 2023, pp. 494-507
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
On stability for generalized linear differential equations and applications to impulsive systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 February 2023, pp. 381-407
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
Cyclicity of rigid centres on centre manifolds of three-dimensional systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 09 February 2023, pp. 188-200
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
SOLUTIONS TO DIFFERENTIAL EQUATIONS VIA FIXED POINT APPROACHES: NEW MATHEMATICAL FOUNDATIONS AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 163-164
- Print publication:
- August 2022
-
- Article
-
- You have access
- HTML
- Export citation