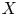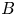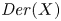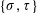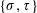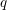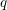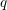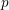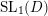38 results in 17Axx
Simplicity of non-associative skew Laurent polynomial rings
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the representability of actions of Leibniz algebras and Poisson algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 22 November 2023, pp. 998-1021
-
- Article
- Export citation
On free subalgebras of varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 November 2021, pp. 89-101
-
- Article
- Export citation
Wick polynomials in noncommutative probability: a group-theoretical approach
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 25 August 2021, pp. 1673-1699
- Print publication:
- December 2022
-
- Article
- Export citation
Algebras with representable representations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 24 June 2021, pp. 555-573
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr theorems for slice regular functions over octonions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 1595-1610
- Print publication:
- October 2021
-
- Article
- Export citation
POTENTIAL ALGEBRAS WITH FEW GENERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 01 July 2020, pp. S28-S76
- Print publication:
- December 2020
-
- Article
- Export citation
ON BASE RADICAL THEORY IN FINITE SETTINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 510-511
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
HOW A NONASSOCIATIVE ALGEBRA REFLECTS THE PROPERTIES OF A SKEW POLYNOMIAL
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 26 November 2019, pp. 6-26
- Print publication:
- January 2021
-
- Article
- Export citation
OPERADIC APPROACH TO COHOMOLOGY OF ASSOCIATIVE TRIPLE AND N-TUPLE SYSTEMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. S128-S141
- Print publication:
- December 2020
-
- Article
- Export citation
α-TYPE CHEVALLEY–EILENBERG COHOMOLOGY OF HOM-LIE ALGEBRAS AND BIALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 03 July 2019, pp. S108-S127
- Print publication:
- December 2020
-
- Article
- Export citation
DIVIDED POWER ALGEBRAS OVER AN OPERAD
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 May 2019, pp. 477-517
- Print publication:
- September 2020
-
- Article
- Export citation
ON REPRESENTATIONS OF SYMMETRIC LEIBNIZ ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 23 May 2019, pp. S99-S107
- Print publication:
- December 2020
-
- Article
- Export citation
CODES, S-STRUCTURES, AND EXCEPTIONAL LIE ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. S14-S27
- Print publication:
- December 2020
-
- Article
- Export citation
Division algebras of slice functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 15 March 2019, pp. 2055-2082
- Print publication:
- August 2020
-
- Article
- Export citation
Duality between p-groups with three characteristic subgroups and semisimple anti-commutative algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 25 February 2019, pp. 1827-1852
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Degenerations of Leibniz and Anticommutative Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 539-549
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
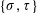 $\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation
$\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 355-372
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
MULTIPLICATION FORMULAS AND SEMISIMPLICITY FOR
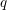 $q$-SCHUR SUPERALGEBRAS
$q$-SCHUR SUPERALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 30 April 2018, pp. 98-126
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
Local–global principle for reduced norms over function fields of
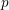 $p$-adic curves
$p$-adic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 02 November 2017, pp. 410-458
- Print publication:
- February 2018
-
- Article
- Export citation