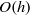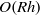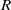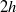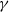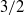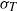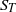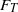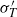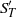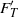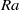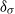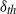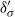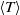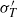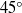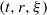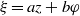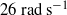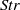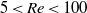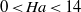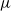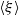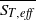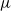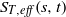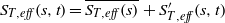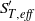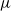Papers
Can barotropic tide–eddy interactions excite internal waves?
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 1-27
-
- Article
-
- You have access
- Open access
- Export citation
Stationary ideal flow on a free surface of a given shape
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 28-45
-
- Article
- Export citation
Study of polygonal water bells: inertia-dominated thin-film flows over microtextured surfaces
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 46-57
-
- Article
- Export citation
The emergence of localized vortex–wave interaction states in plane Couette flow
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 58-85
-
- Article
- Export citation
Rapid gravitational adjustment of horizontal shear flows
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 86-117
-
- Article
- Export citation
A multi-fidelity modelling approach for evaluation and optimization of wing stroke aerodynamics in flapping flight
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 118-154
-
- Article
- Export citation
Effect of turbulent fluctuations on the drag and lift forces on a towed sphere and its boundary layer
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 155-179
-
- Article
- Export citation
Off-plane motion of a prolate capsule in shear flow
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 180-198
-
- Article
- Export citation
Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 199-224
-
- Article
- Export citation
Volume displacement effects during bubble entrainment in a travelling vortex ring
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 225-267
-
- Article
- Export citation
Variable density and viscosity, miscible displacements in horizontal Hele-Shaw cells. Part 1. Linear stability analysis
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 268-294
-
- Article
- Export citation
Variable density and viscosity, miscible displacements in horizontal Hele-Shaw cells. Part 2. Nonlinear simulations
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 295-323
-
- Article
- Export citation
Nonlinear analysis of shock–vortex interaction: Mach stem formation
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 324-339
-
- Article
- Export citation
New conservation laws of helically symmetric, plane and rotationally symmetric viscous and inviscid flows
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 340-366
-
- Article
- Export citation
Ultra-fast escape of a deformable jet-propelled body
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 367-385
-
- Article
- Export citation
Edges in models of shear flow
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 386-402
-
- Article
- Export citation
Transient force generation during impulsive rotation of wall-mounted panels
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 403-437
-
- Article
- Export citation
Visualization of the Ludford column
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 438-453
-
- Article
- Export citation
Large-eddy simulation of three-dimensional dunes in a steady, unidirectional flow. Part 1. Turbulence statistics
-
- Published online by Cambridge University Press:
- 13 March 2013, pp. 454-483
-
- Article
- Export citation
Flame wrinkle destruction processes in harmonically forced, turbulent premixed flames
-
- Published online by Cambridge University Press:
- 19 March 2013, pp. 484-513
-
- Article
- Export citation