Article contents
The emergence of localized vortex–wave interaction states in plane Couette flow
Published online by Cambridge University Press: 13 March 2013
Abstract
The recently understood relationship between high-Reynolds-number vortex–wave interaction theory and computationally generated self-sustaining processes provides a possible route to an understanding of some of the underlying structures of fully turbulent flows. Here vortex–wave interaction (VWI) theory is used in the long streamwise wavelength limit to continue the development found at order-one wavelengths by Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). The asymptotic description given reduces the Navier–Stokes equations to the so-called boundary-region equations, for which we find equilibrium states describing the change in the VWI as the wavelength of the wave increases from 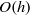 $O(h)$ to
$O(h)$ to 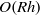 $O(Rh)$, where
$O(Rh)$, where 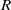 $R$ is the Reynolds number and
$R$ is the Reynolds number and 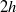 $2h$ is the depth of the channel. The reduced equations do not include the streamwise pressure gradient of the perturbation or the effect of streamwise diffusion of the wave–vortex states. The solutions we calculate have an asymptotic error proportional to
$2h$ is the depth of the channel. The reduced equations do not include the streamwise pressure gradient of the perturbation or the effect of streamwise diffusion of the wave–vortex states. The solutions we calculate have an asymptotic error proportional to 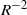 ${R}^{- 2} $ when compared to the full Navier–Stokes equations. The results found correspond to the minimum drag configuration for VWI states and might therefore be of relevance to the control of turbulent flows. The key feature of the new states discussed here is the thickening of the critical layer structure associated with the wave part of the flow to completely fill the channel, so that the roll part of the flow is driven throughout the flow rather than as in Hall & Sherwin as a stress discontinuity across the critical layer. We identify a critical streamwise wavenumber scaling, which, when approached, causes the flow to localize and take on similarities with computationally generated or experimentally observed turbulent spots. In effect, the identification of this critical wavenumber for a given value of the assumed high Reynolds number fixes a minimum box length necessary for the emergence of localized structures. Whereas nonlinear equilibrium states of the Navier–Stokes equations are thought to form a backbone on which turbulent flows hang, our results suggest that the localized states found here might play a related role for turbulent spots.
${R}^{- 2} $ when compared to the full Navier–Stokes equations. The results found correspond to the minimum drag configuration for VWI states and might therefore be of relevance to the control of turbulent flows. The key feature of the new states discussed here is the thickening of the critical layer structure associated with the wave part of the flow to completely fill the channel, so that the roll part of the flow is driven throughout the flow rather than as in Hall & Sherwin as a stress discontinuity across the critical layer. We identify a critical streamwise wavenumber scaling, which, when approached, causes the flow to localize and take on similarities with computationally generated or experimentally observed turbulent spots. In effect, the identification of this critical wavenumber for a given value of the assumed high Reynolds number fixes a minimum box length necessary for the emergence of localized structures. Whereas nonlinear equilibrium states of the Navier–Stokes equations are thought to form a backbone on which turbulent flows hang, our results suggest that the localized states found here might play a related role for turbulent spots.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 45
- Cited by




