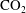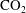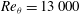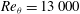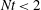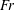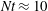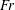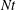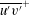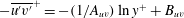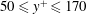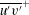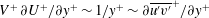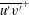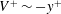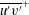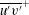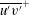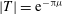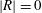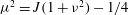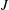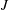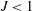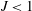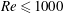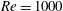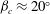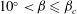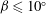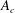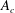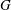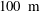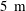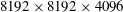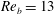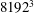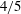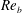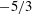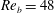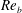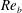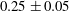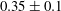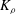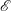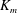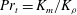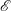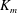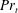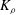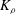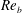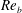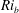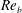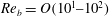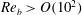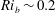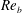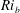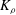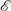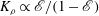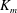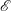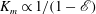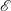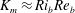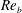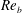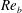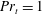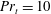In order that it be correctly characterized, irreversible turbulent mixing in stratified fluids must distinguish between adiabatic ‘stirring’ and diabatic ‘mixing’. Such a distinction has been formalized through the definition of a diapycnal diffusivity, 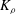 $K_{{\it\rho}}$ (Winters & D’Asaro, J. Fluid Mech., vol. 317, 1996, pp. 179–193) and an appropriate mixing efficiency,
$K_{{\it\rho}}$ (Winters & D’Asaro, J. Fluid Mech., vol. 317, 1996, pp. 179–193) and an appropriate mixing efficiency, 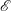 $\mathscr{E}$ (Caulfield & Peltier, J. Fluid Mech., vol. 413, 2000, pp. 1–47). Equivalent attention has not been paid to the definitions of a corresponding momentum diffusivity
$\mathscr{E}$ (Caulfield & Peltier, J. Fluid Mech., vol. 413, 2000, pp. 1–47). Equivalent attention has not been paid to the definitions of a corresponding momentum diffusivity 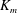 $K_{m}$ and hence an appropriately defined turbulent Prandtl number
$K_{m}$ and hence an appropriately defined turbulent Prandtl number 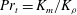 $\mathit{Pr}_{t}=K_{m}/K_{{\it\rho}}$. In this paper, the diascalar framework of Winters & D’Asaro (1996) is first reformulated to obtain an ‘Osborn-like’ formula in which the correct definition of irreversible mixing efficiency
$\mathit{Pr}_{t}=K_{m}/K_{{\it\rho}}$. In this paper, the diascalar framework of Winters & D’Asaro (1996) is first reformulated to obtain an ‘Osborn-like’ formula in which the correct definition of irreversible mixing efficiency 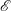 $\mathscr{E}$ is shown to replace the flux Richardson number which Osborn (J. Phys. Oceanogr., vol. 10, 1980, pp. 83–89) assumed to characterize this efficiency. We advocate the use of this revised representation for diapycnal diffusivity since the proposed reformulation effectively removes the simplifying assumptions on which the original Osborn formula was based. We similarly propose correspondingly reasonable definitions for
$\mathscr{E}$ is shown to replace the flux Richardson number which Osborn (J. Phys. Oceanogr., vol. 10, 1980, pp. 83–89) assumed to characterize this efficiency. We advocate the use of this revised representation for diapycnal diffusivity since the proposed reformulation effectively removes the simplifying assumptions on which the original Osborn formula was based. We similarly propose correspondingly reasonable definitions for 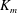 $K_{m}$ and
$K_{m}$ and 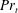 $\mathit{Pr}_{t}$ by eliminating the reversible component of the momentum production term. To explore implications of the reformulations for both diapycnal and momentum diffusivity we employ an extensive series of direct numerical simulations (DNS) to investigate the properties of the shear-induced density-stratified turbulence that is engendered through the breaking of a freely evolving Kelvin–Helmholtz wave. The DNS results based on the proposed reformulation of
$\mathit{Pr}_{t}$ by eliminating the reversible component of the momentum production term. To explore implications of the reformulations for both diapycnal and momentum diffusivity we employ an extensive series of direct numerical simulations (DNS) to investigate the properties of the shear-induced density-stratified turbulence that is engendered through the breaking of a freely evolving Kelvin–Helmholtz wave. The DNS results based on the proposed reformulation of 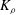 $K_{{\it\rho}}$ are compared with available estimations due to the mixing length model, as well as both the Osborn–Cox and the Osborn models. Estimates based upon the Osborn–Cox formulation are shown to provide the closest approximation to the diapycnal diffusivity delivered by the exact representation. Through compilation of the complete set of DNS results we explore the characteristic dependence of
$K_{{\it\rho}}$ are compared with available estimations due to the mixing length model, as well as both the Osborn–Cox and the Osborn models. Estimates based upon the Osborn–Cox formulation are shown to provide the closest approximation to the diapycnal diffusivity delivered by the exact representation. Through compilation of the complete set of DNS results we explore the characteristic dependence of 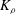 $K_{{\it\rho}}$ on the buoyancy Reynolds number
$K_{{\it\rho}}$ on the buoyancy Reynolds number 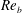 $\mathit{Re}_{b}$ as originally investigated by Shih et al. (J. Fluid Mech., vol. 525, 2005, pp. 193–214) in their idealized study of homogeneous stratified and sheared turbulence, and show that the validity of their results is only further reinforced through analysis of the turbulence produced in the more geophysically relevant Kelvin–Helmholtz wave life-cycle ansatz. In contrast to the results described by Shih et al. (2005) however, we show that, besides
$\mathit{Re}_{b}$ as originally investigated by Shih et al. (J. Fluid Mech., vol. 525, 2005, pp. 193–214) in their idealized study of homogeneous stratified and sheared turbulence, and show that the validity of their results is only further reinforced through analysis of the turbulence produced in the more geophysically relevant Kelvin–Helmholtz wave life-cycle ansatz. In contrast to the results described by Shih et al. (2005) however, we show that, besides 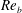 $\mathit{Re}_{b}$, a vertically averaged measure of the gradient Richardson number
$\mathit{Re}_{b}$, a vertically averaged measure of the gradient Richardson number 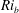 $\mathit{Ri}_{b}$ may equivalently characterize the turbulent mixing at high
$\mathit{Ri}_{b}$ may equivalently characterize the turbulent mixing at high 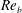 $\mathit{Re}_{b}$. Based on the dominant driving processes involved in irreversible mixing, we categorize the intermediate (i.e.
$\mathit{Re}_{b}$. Based on the dominant driving processes involved in irreversible mixing, we categorize the intermediate (i.e. 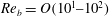 $\mathit{Re}_{b}=O(10^{1}{-}10^{2})$) and high (i.e.
$\mathit{Re}_{b}=O(10^{1}{-}10^{2})$) and high (i.e. 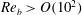 $\mathit{Re}_{b}>O(10^{2})$) range of
$\mathit{Re}_{b}>O(10^{2})$) range of  $\mathit{Re}_{b}$ as ‘buoyancy-dominated’ and ‘shear-dominated’ mixing regimes, which together define a transition value of
$\mathit{Re}_{b}$ as ‘buoyancy-dominated’ and ‘shear-dominated’ mixing regimes, which together define a transition value of 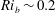 $\mathit{Ri}_{b}\sim 0.2$. Mixing efficiency varies non-monotonically with both
$\mathit{Ri}_{b}\sim 0.2$. Mixing efficiency varies non-monotonically with both 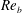 $\mathit{Re}_{b}$ and
$\mathit{Re}_{b}$ and 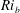 $\mathit{Ri}_{b}$, with its maximum (on the order of 0.2–0.3) occurring in the ‘buoyancy-dominated’ regime. Unlike
$\mathit{Ri}_{b}$, with its maximum (on the order of 0.2–0.3) occurring in the ‘buoyancy-dominated’ regime. Unlike 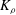 $K_{{\it\rho}}$ which is very sensitive to the correct choice of
$K_{{\it\rho}}$ which is very sensitive to the correct choice of 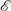 $\mathscr{E}$ (i.e.
$\mathscr{E}$ (i.e. 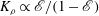 $K_{{\it\rho}}\propto \mathscr{E}/(1-\mathscr{E})$), we show that
$K_{{\it\rho}}\propto \mathscr{E}/(1-\mathscr{E})$), we show that 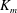 $K_{m}$ is almost insensitive to the choice of
$K_{m}$ is almost insensitive to the choice of 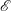 $\mathscr{E}$ (i.e.
$\mathscr{E}$ (i.e. 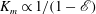 $K_{m}\propto 1/(1-\mathscr{E})$) so long as
$K_{m}\propto 1/(1-\mathscr{E})$) so long as 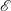 $\mathscr{E}$ is not close to unity, which implies
$\mathscr{E}$ is not close to unity, which implies 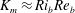 $K_{m}\approx \mathit{Ri}_{b}\mathit{Re}_{b}$ for the entire range of
$K_{m}\approx \mathit{Ri}_{b}\mathit{Re}_{b}$ for the entire range of 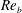 $\mathit{Re}_{b}$. The turbulent Prandtl number is consequently shown to decrease monotonically with
$\mathit{Re}_{b}$. The turbulent Prandtl number is consequently shown to decrease monotonically with 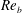 $\mathit{Re}_{b}$ and may be (to first order) simply approximated by
$\mathit{Re}_{b}$ and may be (to first order) simply approximated by 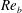 $\mathit{Re}_{b}$ itself. Assuming
$\mathit{Re}_{b}$ itself. Assuming 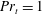 $\mathit{Pr}_{t}=1$, or
$\mathit{Pr}_{t}=1$, or 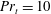 $\mathit{Pr}_{t}=10$ (as is common in large-scale numerical models of the ocean general circulation), is also suggested to be a questionable assumption.
$\mathit{Pr}_{t}=10$ (as is common in large-scale numerical models of the ocean general circulation), is also suggested to be a questionable assumption.
 $\text{CO}_{2}$ spherical cap bubble adhered to a flat surface in air-saturated water
$\text{CO}_{2}$ spherical cap bubble adhered to a flat surface in air-saturated water
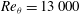 $Re_{{\it\theta}}=13\,000$
$Re_{{\it\theta}}=13\,000$