Hostname: page-component-7479d7b7d-c9gpj Total loading time: 0 Render date: 2024-07-10T13:21:01.290Z Has data issue: false hasContentIssue false
  • English
  • Français

On the scale-dependent turbulent convection velocity in a spatially developing flat plate turbulent boundary layer at Reynolds number 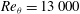$Re_{{\it\theta}}=13\,000$

Published online by Cambridge University Press:  17 June 2015

Nicolas Renard  and
Sébastien Deck
Nicolas Renard
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
Sébastien Deck*
Affiliation:
ONERA, The French Aerospace Lab, F-92190 Meudon, France
*
†Email address for correspondence: sebastien.deck@onera.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The scale-dependent turbulent convection velocity of streamwise velocity fluctuations resolved by large eddy simulation is investigated for the first time across the whole profile of a zero-pressure-gradient spatially developing smooth flat plate boundary layer at 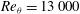$\mathit{Re}_{{\it\theta}}=13\,000$. The high Reynolds number and streamwise heterogeneity constraints motivate the derivation of a dedicated new method to assess the frequency-dependent convection velocity from time signals and their local streamwise derivative, using estimates of power spectral densities (PSDs). This method is inspired by del Álamo & Jiménez (J. Fluid Mech., vol. 640, 2009, pp. 5–26), who treated a lower Reynolds number channel flow with a method suited to spectral direct numerical simulations of streamwise homogeneous flows. Reconstruction of the streamwise spectrum from the time spectrum using the scale-dependent convection velocity is illustrated and compared with classical strategies. The new method inherently includes not only the assessment of the validity of Taylor’s hypothesis, whose trend is remarkably consistent with theoretical predictions by Lin (Q. Appl. Maths, vol. X(4), 1953, 154–165), but also the definition of a global convection velocity accounting for any arbitrary frequency band. This global velocity is shown to coincide with a correlation-based method widely used in experiments. In addition to the mathematical least-squares definition of this velocity, new interpretations based on the flow physics and turbulent micro time scales are presented. Further, the group velocity is assessed and its relation to convection is discussed.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent convection Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 775 , 25 July 2015 , pp. 105 - 148
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Atkinson, C., Buchmann, N. A. & Soria, J. 2015 An experimental investigation of turbulent convection velocities in a turbulent boundary layer. Flow Turbul. Combust. 94, 79–95.Google Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google ScholarPubMed
Blackwelder, R. 1977 On the role of phase information in conditional sampling. Phys. Fluids 20, S232–S242.CrossRefGoogle Scholar
Buxton, O. R. H., de Kat, R. & Ganapathisubramani, B. 2013 The convection of large and intermediate scale fluctuations in a turbulent mixing layer. Phys. Fluids 25, 125105.Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.Google Scholar
Chapman, D. R. 1979 Computational aerodynamics development and outlook. AIAA J. 17 (12), 1293–1313.Google Scholar
Charru, F. 2011 Hydrodynamic Instabilities, Cambridge Texts in Applied Mathematics (No. 37). Cambridge University Press.CrossRefGoogle Scholar
Choi, H. & Moin, P. 1990 On the space–time characteristics of wall-pressure fluctuations. Phys. Fluids 2, 1450–1460.Google Scholar
Choi, H. & Moin, P. 1994 Effects of the computational time step on numerical solutions of turbulent flow. J. Comput. Phys. 113 (1), 227–234.Google Scholar
Choi, H. & Moin, P. 2012 Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 24, 011702.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 574, 25–58.Google Scholar
Davoust, S. & Jacquin, L. 2011 Taylor’s hypothesis convection velocities from mass conservation equation. Phys. Fluids 23, 051701.Google Scholar
Deck, S. 2012 Recent improvements in the Zonal Detached Eddy Simulation (ZDES) formulation. Theor. Comput. Fluid Dyn. 26, 523–550.CrossRefGoogle Scholar
Deck, S. & Laraufie, R. 2013 Numerical investigation of the flow dynamics past a three-element aerofoil. J. Fluid Mech. 732, 401–444.Google Scholar
Deck, S., Renard, N., Laraufie, R. & Sagaut, P. 2014a Zonal detached eddy simulation (ZDES) of a spatially developing flat plate turbulent boundary layer over the Reynolds number range $3150\leqslant Re_{{\it\theta}}\leqslant 14\hspace{2.22198pt}000$ . Phys. Fluids 26, 025116.Google Scholar
Deck, S., Renard, N., Laraufie, R. & Weiss, P.-E. 2014b Large scale contribution to mean wall shear stress in high Reynolds number flat plate boundary layers up to $Re_{{\it\theta}}=13\hspace{2.22198pt}650$ . J. Fluid Mech. 743, 202–248.Google Scholar
Deck, S. & Thorigny, P. 2007 Unsteadiness of an axisymmetric separating–reattaching flow: numerical investigation. Phys. Fluids 19, 065103.CrossRefGoogle Scholar
Deck, S., Weiss, P.-É., Pamiès, M. & Garnier, E. 2011 Zonal Detached Eddy Simulation of a spatially developing flat plate turbulent boundary layer. Comput. Fluids 48, 1–15.Google Scholar
DeGraaff, D. B. & Eaton, J. K. 2000 Reynolds number scaling of the flat plate turbulent boundary layer. J. Fluid Mech. 422, 319–346.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Eitel-Amor, G., Örlü, R. & Schlatter, P. 2014 Simulation and validation of a spatially evolving turbulent boundary layer up to $Re_{{\it\theta}}=8\hspace{2.22198pt}300$ . Intl J. Heat Fluid Flow 47, 57–69.CrossRefGoogle Scholar
Elsinga, G. E., Poelma, C., Schröder, A., Geisler, R., Scarano, F. & Westerweel, J. 2012 Tracking of vortices in a turbulent boundary layer. J. Fluid Mech. 697, 273–295.Google Scholar
Favre, A., Gaviglio, J. & Dumas, R. 1967 Structure of velocity space time correlations in a boundary layer. Phys. Fluids 10, S138–S145.Google Scholar
Fisher, M. J. & Davies, P. O. A. L. 1963 Correlation measurements in a non-frozen pattern of turbulence. J. Fluid Mech. 18, 97–116.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Gand, F., Deck, S., Brunet, V. & Sagaut, P. 2010 Flow dynamics past a simplified wing body junction. Phys. Fluids 22, 115111.CrossRefGoogle Scholar
Goldschmidt, V. W., Young, M. F. & Ott, E. S. 1981 Turbulent convective velocities (broadband and wavenumber dependent) in a plane jet. J. Fluid Mech. 105, 327–345.CrossRefGoogle Scholar
Hinze, J. O. 1959 Turbulence: An Introduction to its Mechanism and Theory. McGraw-Hill.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. C. H. & Marusic, I. 2011 Three-dimensional conditional structure of a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 673, 255–285.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Jarrin, N., Benhamadouche, S., Laurence, D. & Prosser, R. 2006 A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Intl J. Heat Fluid Flow 27, 585–593.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25, 101302.Google Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
de Kat, R., Gan, L., Dawson, J. R. & Ganapathisubramani, B.2012 Limitations of estimating turbulent convection velocities from PIV. In 16th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal.Google Scholar
Kim, J. & Hussain, F. 1993 Propagation velocity of perturbations in turbulent channel flow. Phys. Fluids 5, 695–706.Google Scholar
Krogstad, P.-Å., Kaspersen, J. H. & Rimestad, S. 1998 Convection velocities in a turbulent boundary layer. Phys. Fluids 10 (4), 949–957.Google Scholar
Laraufie, R. & Deck, S. 2013 Assessment of Reynolds stresses tensor reconstruction methods for synthetic turbulent inflow conditions: application to hybrid RANS/LES methods. Intl J. Heat Fluid Flow 42, 68–78.Google Scholar
Laraufie, R., Deck, S. & Sagaut, P. 2011 A dynamic forcing method for unsteady turbulent inflow conditions. J. Comput. Phys. 230, 8647–8663.Google Scholar
Laraufie, R., Deck, S. & Sagaut, P. 2012 A Rapid switch from RANS to WMLES for spatially developing boundary layers. In Progress in Hybrid RANS-LES Modelling, NNFM117 (ed. Fu, S., Haase, W., Peng, S.-H. & Schwamborn, D.), pp. 147–156. Springer.Google Scholar
Larchevêque, L., Sagaut, P., Lê, T.-H. & Comte, P. 2004 Large-eddy simulation of a compressible flow in a three-dimensional open cavity at high Reynolds number. J. Fluid Mech. 516, 265–301.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25, 045103.Google Scholar
LeHew, J., Guala, M. & McKeon, B. J. 2011 A study of the three-dimensional spectral energy distribution in a zero pressure gradient turbulent boundary layer. Exp. Fluids 51, 997–1012.CrossRefGoogle Scholar
LeHew, J. A., Guala, M. & McKeon, B. J. 2013 Time-resolved measurements of coherent structures in the turbulent boundary layer. Exp. Fluids 54, 1508.Google Scholar
Lin, C. C. 1953 On Taylor’s hypothesis and the acceleration terms in the Navier–Stokes equations. Q. Appl. Maths X (4), 154–165.Google Scholar
Marusic, I. & Hutchins, N. 2005 Experimental study of wall turbulence: implications for control. In Transition and Turbulence Control, Lecture Notes Series, vol. 8, pp. 1–40. Institute for Mathematical Sciences, National University of Singapore.CrossRefGoogle Scholar
Marusic, I. & Kunkel, G. J. 2003 Streamwise turbulence intensity formulation for flat-plate boundary layers. Phys. Fluids 15 (8), 2461–2464.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010a High Reynolds number effects in wall turbulence. Intl J. Heat Fluid Flow 31, 418–428.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010b Predictive model for wall-bounded turbulent flow. Science 329, 193–196.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010c Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
Marusic, I., Uddin, A. K. M. & Perry, A. E. 1997 Similarity law for the streamwise turbulence intensity in zero-pressure-gradient turbulent boundary layers. Phys. Fluids 9, 3718–3726.Google Scholar
Mary, I. & Sagaut, P. 2002 Large eddy simulation of flow around an airfoil near stall. AIAA J. 40, 1139–1145.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Mathis, R., Marusic, I., Chernyshenko, S. I. & Hutchins, N. 2013 Estimating wall-shear-stress fluctuations given an outer region input. J. Fluid Mech. 715, 163–180.Google Scholar
Moin, P. 2009 Revisiting Taylor’s hypothesis. J. Fluid Mech. 640, 1–4.Google Scholar
Monty, J. P. & Chong, M. S. 2009 Turbulent channel flow: comparison of streamwise velocity data from experiments and direct numerical simulation. J. Fluid Mech. 633, 461–474.Google Scholar
Pamiès, M., Weiss, P. E., Garnier, E., Deck, S. & Sagaut, P. 2009 Generation of synthetic turbulent inflow data for large eddy simulation of spatially evolving wall-bounded flows. Phys. Fluids 21, 045103.Google Scholar
Piomelli, U. & Balaras, E. 2002 Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 34, 349–374.Google Scholar
Piomelli, U., Balint, J.-L. & Wallace, J. M. 1989 On the validity of Taylor’s hypothesis for wall-bounded flows. Phys. Fluids 1, 609–611.Google Scholar
Pirozzoli, S. & Bernardini, M. 2013 Probing high-Reynolds-number effects in numerical boundary layers. Phys. Fluids 25, 021704.CrossRefGoogle Scholar
Romano, G. P. 1995 Analysis of two-point velocity measurements in near-wall flows. Exp. Fluids 20, 68–83.Google Scholar
Sillero, J., Jiménez, J., Moser, R. D. & Malaya, N. P. 2011 Direct simulation of a zero-pressure-gradient turbulent boundary layer up to $Re_{{\it\theta}}$ = 6650. In 13th European Turbulence Conference (ETC13), J. Phys.: Conference Series, vol. 318. IOP Publishing.Google Scholar
Simon, F., Deck, S., Guillen, P., Sagaut, P. & Merlen, A. 2007 Numerical simulation of the compressible mixing layer past an axisymmetric trailing edge. J. Fluid Mech. 591, 215–253.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. Rapids 746, R1.Google Scholar
Vincenti, P., Klewicki, J., Morrill-Winter, C., White, C. M. & Wosnik, M. 2013 Streamwise velocity statistics in turbulent boundary layers that spatially develop to high Reynolds number. Exp. Fluids 54, 1629.Google Scholar
Weiss, P.-E. & Deck, S. 2011 Control of the antisymmetric mode $(m=1)$ for high Reynolds axisymmetric turbulent separating/reattaching flows. Phys. Fluids 23, 095102.Google Scholar
Weiss, P.-E., Deck, S., Robinet, J.-C. & Sagaut, P. 2009 On the dynamics of axisymmetric turbulent separating/reattaching flows. Phys. Fluids 21, 075103.Google Scholar
Welch, P. D. 1967 The use of Fast Fourier Transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. AU-15 (2), 70–73.CrossRefGoogle Scholar
Wills, J. A. B. 1964 On convection velocities in turbulent shear flows. J. Fluid Mech. 20 (3), 417–432.Google Scholar
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1981 Taylor hypothesis and large-scale coherent structures. J. Fluid Mech. 112, 379–396.Google Scholar