Research Article
An Indefinite Bibasic Summation Formula and Some Quadratic, Cubic and Quartic Summation and Transformation Formulas
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-27
-
- Article
-
- You have access
- Export citation
Codimension 2 Symmetric Homoclinic Bifurcations and Application to 1:2 Resonance
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 191-212
-
- Article
-
- You have access
- Export citation
IP-Sets on the Circle
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 575-589
-
- Article
-
- You have access
- Export citation
On Automorphisms of Complete Algebras And The Isomorphism Problem for Modular Group Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 383-394
-
- Article
-
- You have access
- Export citation
Exact Values for Degree Sums Over Strips of Young Diagrams
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 763-775
-
- Article
-
- You have access
- Export citation
Automorphisms of a Certain Skew Polynomial Ring of Derivation Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 949-958
-
- Article
-
- You have access
- Export citation
The Failure of Cancellation Laws for Equidecomposability Types
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 590-606
-
- Article
-
- You have access
- Export citation
Total Categories and Solid Functors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 213-229
-
- Article
-
- You have access
- Export citation
Generalized Amalgams, With Applications to Fourier Transform
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 395-409
-
- Article
-
- You have access
- Export citation
Commuting Dilations and Uniform Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 776-789
-
- Article
-
- You have access
- Export citation
A Schensted Algorithm Which Models Tensor Representations of the Orthogonal Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 28-49
-
- Article
-
- You have access
- Export citation
Weighted Interpolation Inequalities and Embeddings in Rn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 959-980
-
- Article
-
- You have access
- Export citation
Diameters in Typical Convex Bodies
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-61
-
- Article
-
- You have access
- Export citation
Constructions of Brauer-Severi Varieties and Norm Hypersurfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 230-238
-
- Article
-
- You have access
- Export citation
Positive Forms on Nuclear *-Algebras and Their Integral Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 410-469
-
- Article
-
- You have access
- Export citation
Sur Une Formule de Ramanujan-Bailey
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 607-618
-
- Article
-
- You have access
- Export citation
Eigenvalues of the Curvature Operator for Certain Homogeneous Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 981-999
-
- Article
-
- You have access
- Export citation
Restricting Representations of Completely Solvable Lie Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 790-824
-
- Article
-
- You have access
- Export citation
Universal Varieties Of (0, 1)-Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 470-490
-
- Article
-
- You have access
- Export citation
Explicit Classifications of Some 2-Extensions of a Field of Characteristic Different from 2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 825-855
-
- Article
-
- You have access
- Export citation



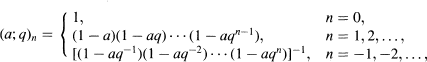
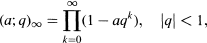
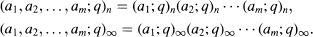
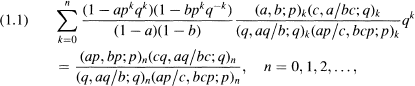
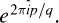 . The map
. The map 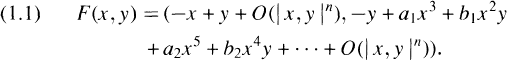
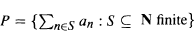 for a certain sequence
for a certain sequence 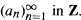 The main questions studied here are : (1) Under what conditions on (
The main questions studied here are : (1) Under what conditions on (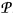 The
The 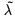 , is the partition (
, is the partition (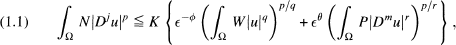
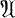 is a self-derivative algebra with an equicontinuous approximate identity, the cone of all positive forms on
is a self-derivative algebra with an equicontinuous approximate identity, the cone of all positive forms on 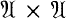 These in turn correspond bijectively to the invariant Hilbert subspaces of the dual space
These in turn correspond bijectively to the invariant Hilbert subspaces of the dual space 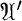 This shows that if
This shows that if 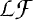 -space, the positive cone of
-space, the positive cone of 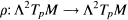
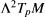 of the tangent space, defined by the formula
of the tangent space, defined by the formula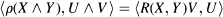
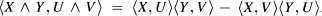 From the symmetries of
From the symmetries of 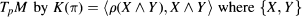 an orthonormal basis of the 2-plane
an orthonormal basis of the 2-plane  be a finite group. Let
be a finite group. Let  , where
, where  the Galois group of
the Galois group of 