Editorial
Editorial
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 169
-
- Article
-
- You have access
- Export citation
Articles
Worldwide Rankings of Research Activity in Econometrics: 1980–1985
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 171-194
-
- Article
- Export citation
Methods for Constructing Top Order Invariant Polynomials
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 195-207
-
- Article
- Export citation
Implications of Aggregation with Common Factors
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 208-222
-
- Article
- Export citation
Full Information Estimations of a System of Simultaneous Equations with Error Component Structure
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 223-246
-
- Article
- Export citation
Approximating the Approximate Slopes of LR, W, and LM Test Statistics
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 247-271
-
- Article
- Export citation
ET Interview
The ET Interview: Professor Edmond Malinvaud: Interviewed by Alberto Holly and Peter C. B. Phillips
- Part of:
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 273-295
-
- Article
- Export citation
A Remark on Magdalinos's k-Class Instrumental Variable Estimator
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 297-298
-
- Article
- Export citation
Preliminary-Test Estimation of the Error Variance in Linear Regression
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 299-304
-
- Article
- Export citation
Problems
Prediction, Extraction, and Estimation in Unobserved Components Models
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 305
-
- Article
- Export citation
Asymptotic Properties of One-Step Estimator Obtained from an Optimal Step Size
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 305-306
-
- Article
- Export citation
A Misspecified Model
-
- Published online by Cambridge University Press:
- 11 February 2009, p. 306
-
- Article
- Export citation
Solutions
Application of Kalman Filter
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 306-309
-
- Article
- Export citation
The Identification and Estimation of a Simple Demand and Supply Model
-
- Published online by Cambridge University Press:
- 11 February 2009, pp. 309-311
-
- Article
- Export citation
Front matter
ECT volume 3 issue 2 Front matter
-
- Published online by Cambridge University Press:
- 11 February 2009, p. f1
-
- Article
-
- You have access
- Export citation

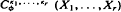 (Davis [8] and Chikuse [2] with
(Davis [8] and Chikuse [2] with 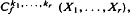 , in which each of the partitions of
, in which each of the partitions of 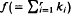 has only one part, occur frequently in multivariate distribution theory (e.g., Hillier and Satchell [17] and Phillips [27]). In this paper we give three methods of constructing these polynomials, extending those of Ruben [28] for the top order zonal polynomials. The first two methods yield explicit formulae for the polynomials and then we give a recurrence procedure. It is shown that some of the expansions presented in Chikuse and Davis [4] are simplified for the top order invariant polynomials. A brief discussion is given on the ‘lowest order’ invariant polynomials.
has only one part, occur frequently in multivariate distribution theory (e.g., Hillier and Satchell [17] and Phillips [27]). In this paper we give three methods of constructing these polynomials, extending those of Ruben [28] for the top order zonal polynomials. The first two methods yield explicit formulae for the polynomials and then we give a recurrence procedure. It is shown that some of the expansions presented in Chikuse and Davis [4] are simplified for the top order invariant polynomials. A brief discussion is given on the ‘lowest order’ invariant polynomials.