Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T14:51:39.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Inhomogeneous parabolic equations on unbounded metric measure spaces

Published online by Cambridge University Press:  20 September 2012

Kenneth J. Falconer ,
Jiaxin Hu  and
Yuhua Sun
Kenneth J. Falconer
Affiliation:
Mathematical Institute, University of St Andrews, North Haugh, St Andrews, Fife KY16 9SS, UK (kjf@st-andrews.ac.uk)
Jiaxin Hu
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, People's Republic of China (hujiaxin@mail.tsinghua.edu.cn; sunyh08@mails.tsinghua.edu.cn)
Yuhua Sun
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, People's Republic of China (hujiaxin@mail.tsinghua.edu.cn; sunyh08@mails.tsinghua.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the inhomogeneous semilinear parabolic equation

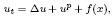
with source term f independent of time and subject to f(x) ≥ 0 and with u(0, x) = φ(x) ≥ 0, for the very general setting of a metric measure space. By establishing Harnack-type inequalities in time t and some powerful estimates, we give sufficient conditions for non-existence, local existence and global existence of weak solutions, depending on the value of p relative to a critical exponent.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 142 , Issue 5 , October 2012 , pp. 1003 - 1025
Copyright
Copyright © Royal Society of Edinburgh 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)