Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-27T13:16:01.768Z Has data issue: false hasContentIssue false
  • English
  • Français

A triple in CAT

Published online by Cambridge University Press:  20 January 2009

Charles Wells
Charles Wells
Affiliation:
Department of Mathematics and StatisticsCase Western Reserve UniversityUniversity CircleCleveland, Ohio, 44106, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A triple (or monad) in a category K is a triple 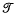= (T, μ, η) where, T: K → K is a functor and μ: TT →, T, η: 1k → T are natural transformations for which (1.1) and (1.2) commute:

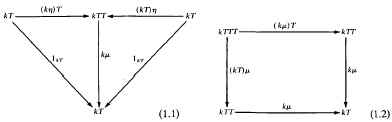
In these diagrams the component of a natural transformation α at an object x is denoted xα. Thus for example (kη)T is the value of the functor T applied to the component of η at k, whereas (kT)η is the component of η at the object kT. I write functions and functors on the right and composition from left to right.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 23 , Issue 3 , October 1980 , pp. 261 - 268
Copyright
Copyright © Edinburgh Mathematical Society 1980

References

REFERENCES

(1)Beck, J., Triples, Algebras and Cohomology (Dissertation, Columbia Univ., 1962), University Microfilms #67–14,023.Google Scholar
(2)Leech, J., ℋ-coextensions of monoids, Mem. Amer. Math. Soc. 157 (1975).Google Scholar
(3)Leech, J., The cohomology of monoids (Preprint).Google Scholar
(4)MacLane, S., Categories for the Working Mathematician (Springer-Verlag, 1971).Google Scholar
(5)Manes, E., Algebraic Theories (Springer-Verlag, 1976).CrossRefGoogle Scholar
(6)Schubert, H., Categories (Springer-Verlag, 1972).CrossRefGoogle Scholar
(7)Wells, C., Extension theories for monoids, Semigroup Forum 16 (1978), 13–35.CrossRefGoogle Scholar