Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T19:38:25.226Z Has data issue: false hasContentIssue false
  • English
  • Français

Electrical transport in the ferromagnetic state of silver substituted manganites La1−xAgxMnO3 (x = 0.05 and 0.1)

Published online by Cambridge University Press:  28 January 2015

Dinesh Varshney ,
Dinesh Choudhary  and
Elias Khan
Dinesh Varshney*
Affiliation:
Materials Science Laboratory, School of Physics, Devi Ahilya University, Indore 452001, India
Dinesh Choudhary
Affiliation:
Materials Science Laboratory, School of Physics, Devi Ahilya University, Indore 452001, India
Elias Khan
Affiliation:
Materials Science Laboratory, School of Physics, Devi Ahilya University, Indore 452001, India
*
a)Address all correspondence to this author. e-mail: vdinesh33@rediffmail.com
Get access

Abstract

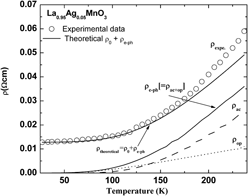
The present study focuses on a quantitative analysis of electrical resistivity in monovalent-doped manganites La1−xAgxMnO3 (x = 0.05 and 0.1). The electrical resistivity data in the ferromagnetic (FM) metallic phase are analyzed by considering a temperature-independent inelastic scattering of the electrons (due to domain and grain boundaries, defects, etc.) and other temperature-dependent elastic scattering mechanisms (electron–electron, electron–phonon, and electron–magnon). The Debye and Einstein temperatures are deduced from the model Hamiltonian containing potential energy contribution from the long-range Coulomb, van der Waals (vdW) interaction, and short-range repulsive interaction up to the second-neighbor ions. The electron–phonon scattering partially describes the reported FM metallic resistivity behavior with temperature for La1−xAgxMnO3 (x = 0.05 and 0.1). The T2 and T4.5 terms accounting for electron–electron and electron–magnon interactions are essential for the correct description of resistivity. The Mott–Ioffe–Regel criterion for metallic conductivity is valid, and kFl ∼ 1, εFτ ∼ 1.

Keywords

manganitesDebye temperaturespin waveselectrical resistivity
Type
Articles
Information
Journal of Materials Research , Volume 30 , Issue 5 , 14 March 2015 , pp. 654 - 665
Copyright
Copyright © Materials Research Society 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Salamon, M.B. and Jaime, M.: The physics of manganites: Structure and transport. Rev. Mod. Phys. 73, 583 (2001).Google Scholar
Zener, C.: Interaction between the d shells in the transition metals. II. Ferromagnetic compounds of manganese with perovskite structure. Phys. Rev. 82, 403 (1951).Google Scholar
Anderson, P.W. and Hasegawa, H.: Considerations on double exchange. Phys. Rev. 100, 675 (1955).Google Scholar
Millis, A.J., Littlewood, P.B., and Shraiman, B.I.: Double exchange alone does not explain the resistivity of La1−xSrxMnO3 . Phys. Rev. Lett. 74, 5144 (1995).Google Scholar
Roy, S., Guo, Y.Q., Venkatesh, S., and Ali, N.: Interplay of structure and transport properties of sodium-doped lanthanum manganite. J. Phys.: Condens. Matter 13, 9547 (2001).Google Scholar
Shannon, R.D.: Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr., Sect. A: Found. Crystallogr. 32, 751 (1976).CrossRefGoogle Scholar
Abrashev, M.V., Litvinchuk, A.P., Iliev, M.N., Meng, R.L., Popov, V.N., Ivanov, V.G., Chakalov, R.A., and Thomsen, C.: Comparative study of optical phonons in the rhombohedrally distorted perovskites LaAlO3 and LaMnO3 . Phys. Rev. B 59, 4146 (1999).Google Scholar
Millis, A.J., Shraiman, B.I., and Mueller, R.: Dynamic Jahn-Teller effect and colossal magnetoresistance in La1−x Sr x MnO3 . Phys. Rev. Lett. 77, 175 (1996).Google Scholar
Sen, C., Alvarez, G., and Dagotto, E.: Competing ferromagnetic and charge-ordered states in models for manganites: The origin of the colossal magnetoresistance effect. Phys. Rev. Lett. 98, 127202 (2007).Google Scholar
Yu, R., Dong, S., Şen, C., Alvarez, G., and Dagotto, E.: Short-range spin and charge correlations and local density of states in the colossal magnetoresistance regime of the single-orbital model for manganites. Phys. Rev. B 77, 214434 (2008).Google Scholar
Ye, S.L., Song, W.H., Dai, J.M., Wang, K.Y., Wang, S.G., Zhang, C.L., Du, J.J., Sun, Y.P., and Fang, J.: Effect of Ag substitution on the transport property and magnetoresistance of LaMnO3 . J. Magn. Magn. Mater. 248, 26 (2002).Google Scholar
Kumar, S. and Majumdar, P.: Singular effect of disorder on electronic transport in strongly coupled electron-phonon systems. Phys. Rev. Lett. 94, 136601 (2005).Google Scholar
Kumar, S. and Majumdar, P.: Insulator-metal phase diagram of the optimally doped manganites from the disordered Holstein-double exchange model. Phys. Rev. Lett. 96, 016602 (2006).Google Scholar
Alexandrov, A.S., Zhao, G-m., Keller, H., Lorenz, B., Wang, Y.S., and Chu, C.W.: Evidence for polaronic Fermi liquid in manganites. Phys. Rev. B 64, 140404 (2001).Google Scholar
Zhao, G-m., Smolyaninova, V., Prellier, W., and Keller, H.: Electrical transport in the ferromagnetic state of manganites: Small-polaron metallic conduction at low temperatures. Phys. Rev. Lett. 84, 6086 (2000).Google Scholar
Jaime, M., Lin, P., Salamon, M.B., and Han, P.D.: Low-temperature electrical transport and double exchange in La0.67(Pb, Ca)0.33MnO3 . Phys. Rev. B. 58, R5901 (1998).Google Scholar
Kubo, K. and Ohata, N.: A quantum theory of double exchange. J. Phys. Soc. Jpn. 33, 21 (1972).Google Scholar
Alexandrov, A.S. and Bratkovsky, A.M.: Carrier density collapse and colossal magnetoresistance in doped manganites. Phys. Rev. Lett. 82, 141 (1999).Google Scholar
Varshney, D. and Kaurav, N.: Electrical resistivity in the ferromagnetic metallic state of La-Ca-MnO3: Role of electron-phonon interaction. Eur. Phys. J. B 40, 129 (2004).Google Scholar
Varshney, D. and Kaurav, N.: Interpretation of temperature-dependent resistivity of La–Pb–MnO3: Role of electron–phonon interaction. J. Low Temp. Phys. 141, 165 (2005).Google Scholar
Varshney, D., Mansuri, I., and Kaurav, N.: Effect of electron/hole doping on the transport properties of lanthanum manganites LaMnO3 . J. Phys.: Condens. Matter 19, 24 (2007).Google Scholar
Varshney, D., Shaikh, M.W., and Mansuri, I.: Interpretation of temperature-dependent resistivity of La0.7Ba0.3MnO3 manganites. J. Alloys Compd. 486, 726 (2009).Google Scholar
Varshney, D., Choudhary, D., and Shaikh, M.W.: Interpretation of metallic and semiconducting temperature dependent resistivity of La1−x Na x MnO3 (x = 0.07, 0.13) manganites. Comput. Mater. Sci. 47, 839 (2010).Google Scholar
Varshney, D., Choudhary, D., and Shaikh, M.W.: Electrical resistivity behavior of sodium substituted manganites: Electron-phonon, electron-electron and electron-magnon interactions. Eur. Phys. J. B 76, 327 (2010).Google Scholar
Iliev, M.N., Abrashev, M.V., Lee, H-G., Popov, V.N., Sun, Y.Y., Thomsen, C., Meng, R.L., and Chu, C.W.: Raman spectroscopy of orthorhombic perovskite like YMnO3 and LaMnO3 . Phys. Rev. B 57, 2872 (1998).Google Scholar
Granado, E., Moreno, N.O., García, A., Sanjurjo, J.A., Rettori, C., Torriani, I., Oseroff, S.B., Neumeier, J.J., McClellan, K.J., Cheong, S-W., and Tokura, Y.: Phonon Raman scattering in R1−xAxMnO3+δ (R = La, Pr; a = Ca, Sr). Phys. Rev. B 58, 11435 (1988).Google Scholar
Tosi, M.P.: Cohesion of ionic solids in the Born model. Solid State Phys. 16, 1 (1964).Google Scholar
Hafemeister, D.W. and Flygare, W.H.: Outer-shell overlap integral as a function of distance for halogen-halogen, halogen-alkali, and alkali-alkali ions in the alkali halide lattices. J. Chem. Phys. 43, 795 (1965).Google Scholar
Slater, J.C. and Kirkwood, J.G.: The van der Waals forces in gases. Phys. Rev. 37, 682 (1931).Google Scholar
Varshney, D., Kaurav, N., Kinge, R., and Singh, R.K.: B1–B2 structural phase transition and elastic properties of UX (X = S, Se, and Te) compounds at high pressure. J. Phys.: Condens. Matter 19, 236204 (2007).Google Scholar
Varshney, D., Joshi, G., Varshney, M., and Shriya, S.: Pressure dependent elastic and structural (B3–B1) properties of Ga based monopnictides. J. Alloys Compd. 495, 23 (2009).Google Scholar
Varshney, D., Rathore, V., Kinge, R., and Singh, R.K.: High-pressure induced structural phase transition in alkaline earth CaX (X = S, Se and Te) semiconductors: NaCl-type (B1) to CsCl-type (B2). J. Alloys Compd. 484, 239 (2009).Google Scholar
Varshney, D., Dagaonkar, G., and Varshney, M.: Pressure and doping dependent elastic and thermodynamical properties of Ga1−x In x P mixed valent compounds. Mater. Res. Bull. 45, 916 (2010).Google Scholar
Varshney, D., Joshi, G., Varshney, M., and Shriya, S.: Pressure induced structural phase transition and elastic properties in BSb, AlSb, GaSb and InSb compounds. Phys. B 405, 1663 (2010).Google Scholar
Varshney, D., Joshi, G., Varshney, M., and Shriya, S.: Pressure induced mechanical properties of boron based pnictides. Solid State Sci. 12, 864 (2010).Google Scholar
Varshney, D., Shriya, S., and Varshney, M.: Study of pressure induced structural phase transition and elastic properties of lanthanum pnictides. Eur. Phys. J. B 85, 241 (2012).Google Scholar
Varshney, D.: Mechanical, and elastic properties of europium mono-oxides and mono-chalcogenides (EuX; X = O, S, Se, Te). Europium: Synthesis, Characteristics and Potential Applications, Attia, M.S., ed.; Nova Science Publication, New York, (2013).Google Scholar
Varshney, D. and Shriya, S.: Elastic, mechanical and thermodynamic properties at high pressures and temperatures of transition metal monocarbides. Int. J. Refract. Met. Hard Mater. 41, 375 (2013).Google Scholar
Millis, A.J.: Cooperative Jahn-Teller effect and electron-phonon coupling in La1−x A x MnO3 . Phys. Rev. B 53, 8434 (1996).Google Scholar
Ederer, C., Lin, C., and Millis, A.J.: Structural distortions and model Hamiltonian parameters: From LSDA to a tight-binding description of LaMnO3 . Phys. Rev. B 76, 155105 (2007).Google Scholar
Varshney, D.: Effect of impurity scatterers on phonon, electron and magnon thermal transport in electron doped cuprate superconductors. Supercond. Sci. Technol. 19, 433 (2006).Google Scholar
Varshney, D. and Mansuri, I.: Influence of Ce doping on structural and transport properties of Ca1−x Ce x MnO3 (x = 0.2) manganite. J. Low Temp. Phys. 162, 52 (2011).Google Scholar
Mansuri, I., Varshney, D., Kaurav, N., Lu, C.L., and Kuo, Y.K.: Effects of A-site disorder on magnetic, electrical and thermal properties of La0.5−x Ln x Ca0.5−y Sr y MnO3 manganites. J. Magn. Magn. Mater. 323, 316 (2011).Google Scholar
Varshney, D., Dodiya, N., and Shaikh, M.W.: Structural properties and electrical resistivity of Na-substituted lanthanum manganites: La1−xNaxMnO3+y (x = 0.1, 0.125 and 0.15). J. Alloys Compd. 509, 7447 (2011).Google Scholar
Varshney, D. and Dodiya, N.: Interpretation of metallic and semiconducting temperature dependent resistivity of La0.91Rb0.06Mn0.94O3 manganites. Solid State Sci. 13, 1623 (2011).Google Scholar
Varshney, D. and Dodiya, N.: Electrical resistivity of the hole doped La0.8Sr0.2MnO3 manganites: Role of electron–electron/phonon/magnon interactions. Mater. Chem. Phys. 129, 896 (2011).Google Scholar
Mansuri, I. and Varshney, D.: Structure and electrical resistivity of La1−xBaxMnO3 (0.25 ≤ x ≤ 0.35) perovskites. J. Alloys Compd. 513, 256 (2012).Google Scholar
Shaikh, M.W. and Varshney, D.: Structural properties and electrical resistivity behavior of La1−x K x MnO3 (x = 0.1, 0.125 and 0.15) manganites. Mater. Chem. Phys. 134, 886 (2012).Google Scholar
Marzari, N. and Vanderbilt, D.: Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847 (1997).Google Scholar
Kamilov, I.K., Gamzatov, A.G., Aliev, A.M., Batdalov, A.B., Abdulvagidov, Sh.B., Mel’nikov, O.V., Gorbenko, O.Yu., and Kaul, A.R.: Kinetic effects in manganites La1−xAgyMnO3 (y ≤ x). J. Exp. Theor. Phys. 105, 774 (2007).Google Scholar
Ghivelder, L., Castillo, I.A., McN Alford, N., Tomka, G.J., Riedi, P.C., MacManus-Driscoll, J., Akther Hossain, A.K.M., and Cohen, L.F.: Specific heat of La1−x Ca x MnO3−δ . J. Magn. Magn. Mater. 189, 274 (1998).Google Scholar
Varshney, D., Mansuri, I., Kaurav, N., Lung, W.Q., and Kuo, Y.K.: Influence of Ce doping on electrical and thermal properties of La0.7−xCexCa0.3MnO3 (0.0 ≤ x ≤0.7) manganites. J. Magn. Magn. Mater. 324, 3276 (2012).Google Scholar
Dodiya, N. and Varshney, D.: Structural properties and Raman spectroscopy of rhombohedral La1−xNaxMnO3 (0.075≤ x ≤0.15). J. Mol. Struct. 1031, 104 (2013).Google Scholar
Varshney, D., Choudhary, D., and Khan, E.: Electrical transport in the ferromagnetic and paramagnetic state of potassium substituted manganites La1−xKxMnO3 (x = 0.05, 0.1 and 0.15). J. Mater. Sci. 48, 5904 (2013).Google Scholar
Varshney, D. and Dodiya, N.: Electrical resistivity of alkali metal doped manganites LaxAyMnwO3 (A = Na, K, Rb): Role of electron-phonon, electron-electron and electron-magnon interactions. Curr. Appl. Phys. 13, 1188 (2013).Google Scholar
Varshney, D., Mansuri, I., Shaikh, M.W., and Kuo, Y.K.: Effect of Fe and Co doping on electrical and thermal properties of La0.5Ce0.5Mn1−x(Fe,Co)xO3 manganites. MRS Bulletin 48, 4606.(2013).Google Scholar
Varshney, D. and Dodiya, N.: Structural and magnetotransport studies of magnetic ion doping for monovalent-doped LaMnO3 manganites. J. Mater. Res. 29, 1183 (2014).Google Scholar
Quijada, M., Cerne, J., Simpson, J.R., Drew, H.D., Ahn, K.H., Millis, A.J., Shreekala, R., Ramesh, R., Rajeswari, M., and Venkatesan, T.: Optical conductivity of manganites: Crossover from Jahn-Teller small polaron to coherent transport in the ferromagnetic state. Phys. Rev. B 58, 16093 (1998).Google Scholar
Urushibara, A., Moritomo, Y., Arima, T., Asamitsu, A., Kido, G., and Tokura, Y.: Insulator-metal transition and giant magnetoresistance in La1−xSrxMnO3 . Phys. Rev. B 51, 14103 (1995).Google Scholar
Egilmez, M., Chow, K.H., Jung, J., Fan, I., Mansour, A.I., and Salman, Z.: Metal-insulator transition, specific heat, and grain-boundary-induced disorder in Sm0.55Sr0.45MnO3 . Appl. Phys. Lett. 92, 132505 (2008).Google Scholar
Mannella, N., Yang, W.L., Tanaka, K., Zhou, X.J., Zheng, H., Mitchell, J.F., Zaanen, J., Devereaux, T.P., Nagaosa, N., Hussain, Z., and Shen, Z.X.: Polaron coherence condensation as the mechanism for colossal magnetoresistance in layered manganites. Phys. Rev. B 76, 233102 (2007).Google Scholar
Mannella, N., Yang, W.L., Zhou, X.J., Zheng, H., Mitchell, J.F., Zaanen, J., Devereaux, T.P., Nagaosa, N., Hussain, Z., and Shen, Z.X.: Nodal quasiparticle in pseudogapped colossal magnetoresistive manganites. Nature 438, 474 (2005).Google Scholar
Graziosi, P., Gambardella, A., Prezioso, M., Riminucci, A., Bergenti, I., Homonnay, N., Schmidt, G., Pullini, D., and Busquets-Mataix, D.: Polaron framework to account for transport properties in metallic epitaxial manganite films. Phys. Rev. B 89, 214411 (2014).Google Scholar
Chen, Z., Xu, Y., Su, Y., Cao, S., and Zhang, J.: Resistivity minimum behavior and weak magnetic disorder characteristics in La2/3Ca1/3MnO3 manganites. J. Supercond. Novel Magn. 22, 465 (2009).Google Scholar
Schiffer, P., Ramirez, A.P., Bao, W., and Cheong, S-W.: Low temperature magnetoresistance and the magnetic phase diagram of La1−xCaxMnO3 . Phys. Rev. Lett. 75, 3335 (1995).Google Scholar
Ang, R., Sun, Y.P., Yang, J., Zhu, X.B., and Song, W.H.: Transport mechanism and magnetothermoelectric power of electron-doped manganites La0.85Te0.15Mn1−xCuxO3 (0 ≤ x ≤ 0.2). J. Appl. Phys. 100, 073706 (2006).Google Scholar
De Teresa, J.M., Ibarra, M.R., Blasco, J., García, J., Marquina, C., and Algarabel, P.A., Arnold, Z. and Kamenev, K., Ritter, C., and von Helmolt, R.: Spontaneous behavior and magnetic field and pressure effects on La2/3Ca1/3MnO3 perovskite. Phys. Rev. B 54, 1187 (1996).Google Scholar