Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-23T13:48:12.774Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE IDEAL CLASS GROUP OF CERTAIN QUADRATIC FIELDS

Published online by Cambridge University Press:  25 August 2010

YASUHIRO KISHI
YASUHIRO KISHI*
Affiliation:
Department of Mathematics, Fukuoka University of Education, 1-1 Bunkyoumachi Akama, Munakata-shi, Fukuoka 811-4192, Japan e-mail: ykishi@fukuoka-edu.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let n(≥ 3) be an odd integer. Let k:= 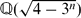be the imaginary quadratic field and k′:= 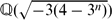the real quadratic field. In this paper, we prove that the class number of k is divisible by 3 unconditionally, and the class number of k′ is divisible by 3 if n(≥ 9) is divisible by 3. Moreover, we prove that the 3-rank of the ideal class group of k is at least 2 if n(≥ 9) is divisible by 3.

Keywords

11R1111R29
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue 3 , September 2010 , pp. 575 - 581
Copyright
Copyright © Glasgow Mathematical Journal Trust 2010

References

REFERENCES

1.Erickson, C., Kaplan, N., Mendoza, N., Pacelli, A. M and Shayler, T., Parameterized families of quadratic number fields with 3-rank at least 2, Acta Arith. 130 (2007), 141–147.CrossRefGoogle Scholar
2.Hasse, H., Arithmetische Theorie der kubischen Zahlkörper auf klassenkörpertheoretischer Grundlage, Math. Z. 31 (1930), 565–582.CrossRefGoogle Scholar
3.Kishi, Y., A criterion for a certain type of imaginary quadratic fields to have 3-ranks of the ideal class groups greater than one, Proc. Japan Acad. Ser. A Math. Sci. 74 (1998), 93–97.CrossRefGoogle Scholar
4.Kishi, Y., A constructive approach to Spiegelung relations between 3-ranks of absolute ideal class groups and congruent ones modulo (3)2 in quadratic fields, J. Number Theory 83 (2000), 1–49.CrossRefGoogle Scholar
5.Kishi, Y., Note on the divisibility of the class number of certain imaginary quadratic fields, Glasgow Math. J. 51 (2009), 187–191.CrossRefGoogle Scholar
6.Kishi, Y. and Miyake, K., Parametrization of the quadratic fields whose class numbers are divisible by three, J. Number Theory 80 (2000), 209–217.CrossRefGoogle Scholar
7.Llorente, P. and Nart, E., Effective determination of the decomposition of the rational primes in a cubic field, Proc. Amer. Math. Soc. 87 (1983), 579–585.CrossRefGoogle Scholar
8.Scholz, A., Über die Beziehung der Klassenzahl quadratischer Körper zueinander, J. Reine Angew. Math. 166 (1932), 201–203.CrossRefGoogle Scholar
9.Yamamoto, Y., On unramified Galois extensions of quadratic number fields, Osaka J. Math. 7 (1970), 57–76.Google Scholar