Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-18T05:39:59.747Z Has data issue: false hasContentIssue false
  • English
  • Français

Convolution with Odd Kernels Having a Tempered Singularity

Published online by Cambridge University Press:  20 November 2018

R. A. Kerman
R. A. Kerman*
Affiliation:
Department of Mathematics, Brock University, St. Catharines, Ontario, L2S 3A1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose b(t) decreases to 0 on [1, ∞). Define the singular integral operator Cb at periodic f of period 1 in L1 (T),T = ( - 1 / 2, 1/2), by

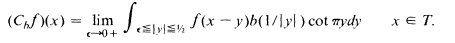
Then, for a large class of b one has the rearrangement inequality

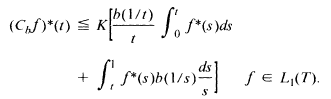
This inequality is used to construct a rearrangement invariant function space X corresponding to a given such space Y so that Cb maps X into Y.

Keywords

42A5046E30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 1 , 01 March 1988 , pp. 3 - 12
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Bennett, C. and Rudnick, K., On Lorentz-Zygmund spaces, Dissertationes Math. 175 (1980), 67 p.Google Scholar
2. Boyd, D. W., Indices of function spaces and their relationship to interpolation, Canad. J. Math. 21 (1969), pp. 1245–1254.Google Scholar
3. Bradley, J. S., Hardy inequalities with mixed norms, Canad. Math. Bull. 21 (1978), pp. 405–408.Google Scholar
4. Calderôn, A. P., Spaces between L and L°° and the theorem of Marcinkiewicz, Studia Math. 26 (1966), pp. 273–299.Google Scholar
5. Hardy, G. H., Littlewood, J. E., and Polya, G., Inequalities, Cambridge Univ. Press, Cambridge, 1934.Google Scholar
6. Kerman, R. A., Function spaces continuously paired by operators of convolution-type, Canad. Math. Bull. 22 (1979), pp. 499–507.Google Scholar
7. Kerman, R. A., An integral extrapolation theorem with applications, Studia Math. 76 (1983), pp. 183–195.Google Scholar
8. Lorentz, G. G., On the theory of spaces Λ, Pacific J. Math. 1 (1951), pp. 411–429.Google Scholar
9. O'Neil, R., Convolution operators and L(p, q) spaces, Duke Math. J. 30 (1963), pp. 129–142.Google Scholar
10. O'Neil, R., Convolution with odd kernels, Studia Math. 44 (1972), pp. 517–526.Google Scholar
11. O'Neil, R. and Weiss, G., The Hilbert transform and rearrangement of functions, Studia Math. 23 (1963), pp. 189–198.Google Scholar
12. Zygmund, A., Trigonometric Series, Vol. I, Cambridge Univ. Press, Cambridge, 1959.Google Scholar