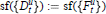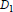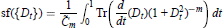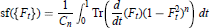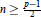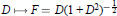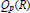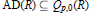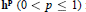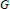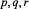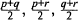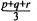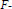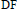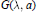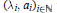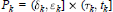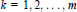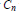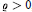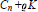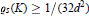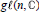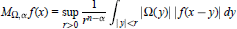Research Article
Derivations and Invariant Forms of Lie Algebras Graded by Finite Root Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-241
-
- Article
-
- You have access
- Export citation
Unbounded Fredholm Modules and Spectral Flow
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-718
-
- Article
-
- You have access
- Export citation
Subgroups of the Adjoint Group of a Radical Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-15
-
- Article
-
- You have access
- Export citation
Qp Spaces on Riemann Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-464
-
- Article
-
- You have access
- Export citation
Ward’s Solitons II: Exact Solutions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1119-1137
-
- Article
-
- You have access
- Export citation
Fourier Multipliers For Local Hardy Spaces On Chébli-Trimèche Hypergroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-928
-
- Article
-
- You have access
- Export citation
Decomposition Varieties in Semisimple Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 929-971
-
- Article
-
- You have access
- Export citation
Indecomposable Almost Free Modules—The Local Case
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 719-738
-
- Article
-
- You have access
- Export citation
Six Primes and an Almost Prime in Four Linear Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 465-486
-
- Article
-
- You have access
- Export citation
Compound Invariants and Mixed F-, DF-Power Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1138-1162
-
- Article
-
- You have access
- Export citation
Intégration Du Sous-Différentiel Proximal: Un Contre Exemple
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 242-265
-
- Article
-
- You have access
- Export citation
Asymptotic Shape of Finite Packings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 16-28
-
- Article
-
- You have access
- Export citation
Gradient Estimates for Harmonic Functions on Manifolds With Lipschitz Metrics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1163-1175
-
- Article
-
- You have access
- Export citation
Eigenpolytopes of Distance Regular Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 739-755
-
- Article
-
- You have access
- Export citation
On the Liouville Property for Divergence Form Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 487-496
-
- Article
-
- You have access
- Export citation
Trace Class Elements and Cross-Sections in Kac-Moody Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 972-1006
-
- Article
-
- You have access
- Export citation
The Torsion Free Pieri Formula
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 266-289
-
- Article
-
- You have access
- Export citation
Weighted Norm Inequalities for Fractional Integral Operators With Rough Kernel
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-39
-
- Article
-
- You have access
- Export citation
Isomorphism Problem for Metacirculant Graphs of Order a Product of Distinct Primes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1176-1188
-
- Article
-
- You have access
- Export citation
Morse Index of Approximating Periodic Solutions for the Billiard Problem. Application to Existence Results
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 497-524
-
- Article
-
- You have access
- Export citation