Article contents
Qp Spaces on Riemann Surfaces
Published online by Cambridge University Press: 20 November 2018
Abstract
We study the function spaces 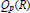 ${{Q}_{p}}(R)$ defined on a Riemann surface
${{Q}_{p}}(R)$ defined on a Riemann surface 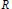 $R$, which were earlier introduced in the unit disk of the complex plane. The nesting property
$R$, which were earlier introduced in the unit disk of the complex plane. The nesting property 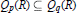 ${{Q}_{p}}(R)\,\subseteq \,{{Q}_{_{q}}}(R)$ for
${{Q}_{p}}(R)\,\subseteq \,{{Q}_{_{q}}}(R)$ for  $0\,<\,p\,<\,q\,<\,\infty $ is shown in case of arbitrary hyperbolic Riemann surfaces. Further, it is proved that the classical Dirichlet space
$0\,<\,p\,<\,q\,<\,\infty $ is shown in case of arbitrary hyperbolic Riemann surfaces. Further, it is proved that the classical Dirichlet space 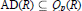 $\text{AD(}R\text{)}\,\subseteq \,{{Q}_{p}}(R)$ for any
$\text{AD(}R\text{)}\,\subseteq \,{{Q}_{p}}(R)$ for any 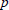 $p$,
$p$, 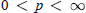 $0\,<\,p\,<\,\infty $, thus sharpening T. Metzger's well-known result
$0\,<\,p\,<\,\infty $, thus sharpening T. Metzger's well-known result 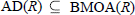 $\text{AD(}R\text{)}\,\subseteq \,\text{BMOA}(R)$. Also the first author's result
$\text{AD(}R\text{)}\,\subseteq \,\text{BMOA}(R)$. Also the first author's result 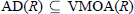 $\text{AD}(R)\,\subseteq \,\text{VMOA}(R)$ for a regular Riemann surface
$\text{AD}(R)\,\subseteq \,\text{VMOA}(R)$ for a regular Riemann surface 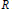 $R$ is sharpened by showing that, in fact,
$R$ is sharpened by showing that, in fact, 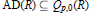 $\text{AD(}R\text{)}\,\subseteq \,{{Q}_{p,0}}(R)$ for all
$\text{AD(}R\text{)}\,\subseteq \,{{Q}_{p,0}}(R)$ for all 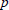 $p$,
$p$, 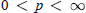 $0\,<\,p\,<\,\infty $. The relationships between
$0\,<\,p\,<\,\infty $. The relationships between 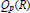 ${{Q}_{p}}(R)$ and various generalizations of the Bloch space on
${{Q}_{p}}(R)$ and various generalizations of the Bloch space on 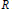 $R$ are considered. Finally we show that
$R$ are considered. Finally we show that 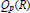 ${{Q}_{p}}(R)$ is a Banach space for
${{Q}_{p}}(R)$ is a Banach space for 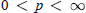 $0\,<\,p\,<\,\infty $.
$0\,<\,p\,<\,\infty $.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 9
- Cited by




