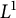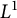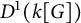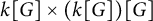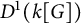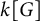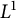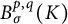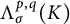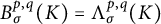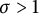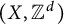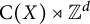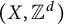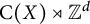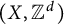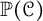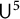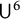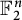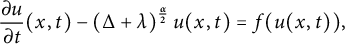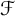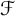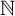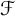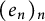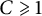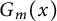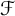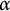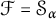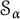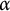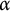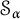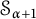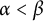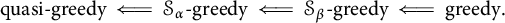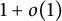Article
Stable finiteness of twisted group rings and noisy linear cellular automata
- Part of:
-
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1089-1108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equivalence of Besov spaces on p.c.f. self-similar sets
- Part of:
-
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1109-1143
-
- Article
-
- You have access
- HTML
- Export citation
The first-order theory of binary overlap-free words is decidable
- Part of:
-
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1144-1162
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bi-free entropy with respect to completely positive maps
- Part of:
-
- Published online by Cambridge University Press:
- 05 June 2023, pp. 1163-1239
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radius of comparison and mean topological dimension:
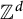 $\mathbb Z^d$-actions
$\mathbb Z^d$-actions
- Part of:
-
- Published online by Cambridge University Press:
- 19 June 2023, pp. 1240-1266
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cobordism distance on the projective space of the knot concordance group
-
- Published online by Cambridge University Press:
- 27 June 2023, pp. 1267-1288
-
- Article
-
- You have access
- HTML
- Export citation
Quantitative inverse theorem for Gowers uniformity norms
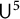 $\mathsf {U}^5$ and
$\mathsf {U}^5$ and 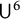 $\mathsf {U}^6$ in
$\mathsf {U}^6$ in 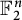 $\mathbb {F}_2^n$
$\mathbb {F}_2^n$
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2023, pp. 1289-1338
-
- Article
-
- You have access
- HTML
- Export citation
Some asymptotic formulae for torsion in homotopy groups
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2023, pp. 1339-1357
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sliding methods for tempered fractional parabolic problem
- Part of:
-
- Published online by Cambridge University Press:
- 28 July 2023, pp. 1358-1378
-
- Article
-
- You have access
- HTML
- Export citation
Schreier families and
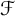 $\mathcal {F}$-(almost) greedy bases
$\mathcal {F}$-(almost) greedy bases
- Part of:
-
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1379-1399
-
- Article
-
- You have access
- HTML
- Export citation
Sensitivity of mixing times of Cayley graphs
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2023, pp. 1400-1431
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the period of Li, Pertusi, and Zhao’s symplectic variety
- Part of:
-
- Published online by Cambridge University Press:
- 04 August 2023, pp. 1432-1453
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
CJM volume 76 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
CJM volume 76 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 30 September 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation