Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-07-02T08:16:33.552Z Has data issue: false hasContentIssue false
  • English
  • Français

Cobordism distance on the projective space of the knot concordance group

Published online by Cambridge University Press:  27 June 2023

Charles Livingston
Charles Livingston*
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN 47405, USA
*
e-mail: livingst@indiana.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We use the cobordism distance on the smooth knot concordance group 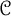$\mathcal {C}$ to measure how close two knots are to being linearly dependent. Our measure, 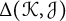$\Delta (\mathcal {K}, \mathcal {J})$, is built by minimizing the cobordism distance between all pairs of knots, 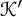$\mathcal {K}'$ and 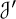$\mathcal {J}'$, in cyclic subgroups containing 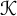$\mathcal {K}$ and 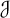$\mathcal {J}$. When made precise, this leads to the definition of the projective space of the concordance group, 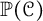${\mathbb P}(\mathcal {C})$, upon which 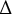$\Delta $ defines an integer-valued metric. We explore basic properties of 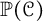${\mathbb P}(\mathcal {C})$ by using torus knots 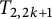$T_{2,2k+1}$. Twist knots are used to demonstrate that the natural simplicial complex 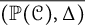$\overline {({\mathbb P}(\mathcal {C}), \Delta )}$ associated with the metric space 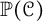${\mathbb P}(\mathcal {C})$ is infinite-dimensional.

Keywords

Knot concordance4-genusalgebraic concordance
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 22
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by a grant from the National Science Foundation (Grant No. NSF-DMS-1505586).

References

Baader, S., Note on crossing changes . Q. J. Math. 57(2006), no. 2, 139–142.10.1093/qmath/hai010CrossRefGoogle Scholar
Baader, S., Scissor equivalence for torus links . Bull. Lond. Math. Soc. 44(2012), no. 5, 1068–1078.10.1112/blms/bds044CrossRefGoogle Scholar
Casson, A. J. and Gordon, C. M. A., Cobordism of classical knots . In: À la recherche de la topologie perdue, Progress in Mathematics, 62, Birkhäuser, Boston, MA, 1986, pp. 181–199, with an appendix by P. M. Gilmer.Google Scholar
Endo, H., Linear independence of topologically slice knots in the smooth cobordism group . Topology Appl. 63(1995), no. 3, 257–262.10.1016/0166-8641(94)00062-8CrossRefGoogle Scholar
Feller, P. and Krcatovich, D., On cobordisms between knots, braid index, and the upsilon-invariant . Math. Ann. 369(2017), nos. 1–2, 301–329.10.1007/s00208-017-1519-1CrossRefGoogle Scholar
Feller, P. and Park, J., Genus one cobordisms between torus knots . Int. Math. Res. Not. IMRN 1(2021), 523–550.Google Scholar
Feller, P. and Park, J., A note on the four-dimensional clasp number of knots . Math. Proc. Camb. Philos. Soc. 173(2022), no. 1, 213–226.10.1017/S0305004121000529CrossRefGoogle Scholar
Fox, R. and Milnor, J., Singularities of $2$ -spheres in $4$ -space and cobordism of knots . Osaka J. Math. 3(1966), 257–267.Google Scholar
Friedl, S., Livingston, C., and Zentner, R., Knot concordances and alternating knots . Michigan Math. J. 66(2017), no. 2, 421–432.10.1307/mmj/1491465685CrossRefGoogle Scholar
Hausmann, J.-C., On the Vietoris–Rips complexes and a cohomology theory for metric spaces . In: Prospects in topology (Princeton, NJ, 1994), Annals of Mathematics Studies, 138, Princeton University Press, Princeton, NJ, 1995, pp. 175–188.Google Scholar
Hedden, M., Notions of positivity and the Ozsváth–Szabó concordance invariant . J. Knot Theory Ramifications 19(2010), no. 5, 617–629.10.1142/S0218216510008017CrossRefGoogle Scholar
Hendricks, K. and Manolescu, C., Involutive Heegaard Floer homology . Duke Math. J. 166(2017), no. 7, 1211–1299.10.1215/00127094-3793141CrossRefGoogle Scholar
Hirasawa, M. and Uchida, Y., The Gordian complex of knots . J. Knot Theory Ramifications 11(2002), no. 3, 363–368.Google Scholar
Jiang, B., A simple proof that the concordance group of algebraically slice knots is infinitely generated . Proc. Amer. Math. Soc. 83(1981), no. 1, 189–192.10.1090/S0002-9939-1981-0620010-7CrossRefGoogle Scholar
Levine, J., Invariants of knot cobordism , Invent. Math. 8(1969), 98–110; addendum, ibid. 8(1969), 355.10.1007/BF01404613CrossRefGoogle Scholar
Lisca, P., Sums of lens spaces bounding rational balls . Algebr. Geom. Topol. 7(2007), 2141–2164.10.2140/agt.2007.7.2141CrossRefGoogle Scholar
Livingston, C., Order 2 algebraically slice knots . In: Proceedings of the Kirbyfest (Berkeley, CA, 1998), Geometry & Topology Monographs, 2, Geometry & Topology Publications, Coventry, 1999, pp. 335–342.Google Scholar
Milnor, J., Infinite cyclic coverings . In: Conference on the topology of manifolds (Michigan State University, East Lansing, MI, 1967), Prindle, Weber & Schmidt, Boston, MA, 1968, pp. 115–133.Google Scholar
Murasugi, K., On a certain numerical invariant of link types . Trans. Amer. Math. Soc. 117(1965), 387–422.10.1090/S0002-9947-1965-0171275-5CrossRefGoogle Scholar
Ozsváth, P. and Szabó, Z., Knot Floer homology and the four-ball genus . Geom. Topol. 7(2003), 615–639.10.2140/gt.2003.7.615CrossRefGoogle Scholar
Rasmussen, J., Khovanov homology and the slice genus . Invent. Math. 182(2010), no. 2, 419–447.10.1007/s00222-010-0275-6CrossRefGoogle Scholar
Rudolph, L., Quasipositivity as an obstruction to sliceness . Bull. Amer. Math. Soc. (N.S.) 29(1993), no. 1, 51–59.10.1090/S0273-0979-1993-00397-5CrossRefGoogle Scholar
Tristram, A., Some cobordism invariants for links . Proc. Camb. Philos. Soc. 66(1969), 251–264.10.1017/S0305004100044947CrossRefGoogle Scholar
Viro, O., Branched coverings of manifolds with boundary, and invariants of links. I . Izv. Akad. Nauk SSSR Ser. Mat. 37(1973), 1241–1258.Google Scholar