Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-19T16:58:30.223Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Strongly Regular Function Algebras

Published online by Cambridge University Press:  20 November 2018

Donald R. Wilken
Donald R. Wilken*
Affiliation:
Massachusetts Institute of Technology, Cambridge, Massachusetts
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a uniformly closed subalgebra of C(X), the algebra of all complex-valued continuous functions on a compact Hausdorff space X. If A separates the points of X and contains the constant functions, A is called a function algebra. The algebra A is said to be strongly regular on X if it has the following property.

Property. For each f in A, each point x in X, and every 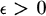, there is a neighbourhood U of x and a function g in A with g(y) = f(x) for all y in U and 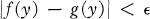for all y in X.

That is, each function in A is uniformly approximate on X by functions in A which are constant near any point of X. Stated in terms of ideals, strong regularity means that, for each x, the ideal of functions vanishing in a neighbourhood of x is uniformly dense in the maximal ideal at x.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 912 - 914
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Bishop, E., Holomorphic completions, analytic continuation, and the interpolation of seminorms, Ann. of Math. (2) 78 (1963), 468–500.Google Scholar
2. Glicksberg, I., Measures orthogonal to algebras and sets of antisymmetry, Trans. Amer. Math. Soc. 105 (1962), 415–435.Google Scholar
3. McKissick, R., A nontrivial normal sup-norm algebra, Bull. Amer. Math. Soc. 69 (1963), 391–395.Google Scholar
4. Wermer, J., Banach algebras and analytic functions, Advances in Math. 1 (1961), fasc. 1, 51–102.Google Scholar
5. Wilken, D. R., Approximate normality and function algebras on the interval and the circle. (Function algebras) pp. 98–111, Proc. Internat. Sympos. on Function Algebras, Tulane Univ., 1965(Scott-Foresman, Chicago, Illinois, 1966).Google Scholar