Correction
Correction to “Arithmetic Linear Transformations”
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-5
-
- Article
-
- You have access
- Export citation
Research Article
The Bracket Function and Complementary Sets of Integers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 6-27
-
- Article
-
- You have access
- Export citation
Unitary Representations of Generalized Symmetric Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 28-38
-
- Article
-
- You have access
- Export citation
Projective Modules Over Central Separable Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-43
-
- Article
-
- You have access
- Export citation
On Projective Modules and Automorphisms of Central Separable Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 44-53
-
- Article
-
- You have access
- Export citation
An Analogue of a Problem of J. Balázs and P. Turán
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-63
-
- Article
-
- You have access
- Export citation
Characterizations of Finite Projective and Affine Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 64-75
-
- Article
-
- You have access
- Export citation
Hjelmslev Planes Derived from Modular Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 76-83
-
- Article
-
- You have access
- Export citation
The Fredholm Elements of a Ring
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 84-95
-
- Article
-
- You have access
- Export citation
Complete Regularity as a Separation Axiom
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 96-105
-
- Article
-
- You have access
- Export citation
Two-Dimensional Linear Groups Over Local Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 106-135
-
- Article
-
- You have access
- Export citation
A Characterization of Intrinsic Functions on
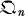
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 136-146
-
- Article
-
- You have access
- Export citation
A Note on Non-Distributive Sublattices of Degrees and Hyperdegrees
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 147-148
-
- Article
-
- You have access
- Export citation
Generalization of Hölder's Theorem to Ordered Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 149-157
-
- Article
-
- You have access
- Export citation
Topologies on Generalized Inner Product Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 158-169
-
- Article
-
- You have access
- Export citation
Structure Theory for Montgomery-Samelson Fiberings between Manifolds. I
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 170-179
-
- Article
-
- You have access
- Export citation
Structure Theory for Montgomery-Samelson Fiberings between Manifolds, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 180-186
-
- Article
-
- You have access
- Export citation
Absolute Convergence Factors for Hp Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 187-195
-
- Article
-
- You have access
- Export citation
Normal Completions of Small Categories
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 196-201
-
- Article
-
- You have access
- Export citation
Decomposition of Metric Spaces with a 0-Dimensional Set of Non-Degenerate Elements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 202-216
-
- Article
-
- You have access
- Export citation



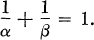
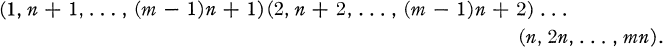
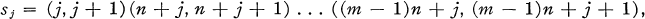
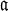 , attach certain congruence groups
, attach certain congruence groups 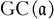 and
and 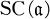 . Next, assign a certain ideal (called the
. Next, assign a certain ideal (called the 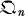
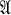 be an associative algebra over the field
be an associative algebra over the field 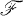 and let
and let 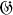 be the group of all automorphisms and anti-automorphisms of
be the group of all automorphisms and anti-automorphisms of 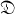 and range contained in
and range contained in 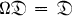 for each Ω in
for each Ω in 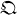 of real quaternions, the algebra
of real quaternions, the algebra 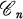 of
of 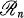 of
of  of
of 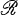 or
or 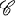 ; see (
; see (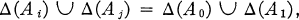
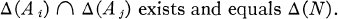
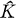 , the topological completion of
, the topological completion of 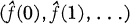 of Fourier coefficients satisfies
of Fourier coefficients satisfies 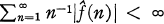 . For this reason we say that the sequence (1, 1/2, 1/3, …) belongs to the multiplier class (H
. For this reason we say that the sequence (1, 1/2, 1/3, …) belongs to the multiplier class (H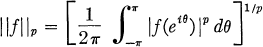
 mean that
mean that 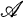 is a full subcategory of
is a full subcategory of 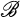 . Moreover, if
. Moreover, if 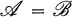 means that each object of
means that each object of