Research Article
Some applications of differential subordination
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-330
-
- Article
-
- You have access
- Export citation
On the volume and projection of convex sets containing no lattice points
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 331-338
-
- Article
-
- You have access
- Export citation
A note on positive semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 339-343
-
- Article
-
- You have access
- Export citation
The near-ring of generalized affine transformations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 345-349
-
- Article
-
- You have access
- Export citation
Some results on k-quasi-hyponormal operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 351-355
-
- Article
-
- You have access
- Export citation
Weakly prime left ideals in general rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-360
-
- Article
-
- You have access
- Export citation
Essential completions of distributive lattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 361-374
-
- Article
-
- You have access
- Export citation
A Strengthened topological cardinal inequality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 375-378
-
- Article
-
- You have access
- Export citation
On a conjecture of Littlewood in Diophantine approximations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 379-387
-
- Article
-
- You have access
- Export citation
Non-existence of odd periodic maps on certain spaces without fixed points
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 389-397
-
- Article
-
- You have access
- Export citation
Finite groups with large centralizers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 399-414
-
- Article
-
- You have access
- Export citation
Derivations on commutative operator algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 415-418
-
- Article
-
- You have access
- Export citation
K-Fold symmetric starlike univalent functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-436
-
- Article
-
- You have access
- Export citation
Some recent results for heat-diffusion moving boundary problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 437-460
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian phD Thesis
Covering the integers with arithmetic progressions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 461-463
-
- Article
-
- You have access
- Export citation
Rotating magnetic upper-main sequence stars
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-467
-
- Article
-
- You have access
- Export citation
A Mathematical and computer simulation model of the running athlete
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 469-472
-
- Article
-
- You have access
- Export citation
Cluster analysis via normal mixture models
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 473-475
-
- Article
-
- You have access
- Export citation
The PhD education of industrial mathematicians in Australia
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-479
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 32 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation

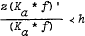 , where
, where 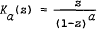 (a real),
(a real), 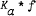 denotes the Hadamard product of
denotes the Hadamard product of 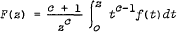 . It is proved that
. It is proved that 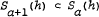 for
for 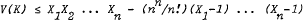
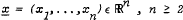 , and any ε > 0 there exist
, and any ε > 0 there exist 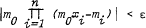 . In this paper we show this conjecture holds for all
. In this paper we show this conjecture holds for all 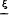
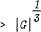 if, for example, |
if, for example, |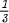 can be improved to
can be improved to 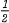 , for example when
, for example when 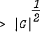 whenever
whenever 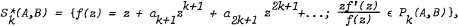
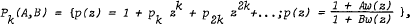
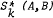 are also derived.
are also derived.